7. Conclusions
This chapter summarises the main conclusions from the previous
chapters (indicated by  ) and gives suggestions for further
research (indicated by
) and gives suggestions for further
research (indicated by
 ).
).
In chapter 2 we demonstrated that driving rain is a
complex phenomenon of falling raindrops in the turbulent flow of wind
around a building. Every individual drop has its individual drop
trajectory. The lifetime of a drop is affected by drop interaction
(collision and breakup) and the environment (wind and evaporation).
However, in our ``theoretical model'' the onslaught of individual
raindrops on a façade depends only on the wind field nearby the
building. In our ``empirical model'' we define the onslaught in terms
of driving rain intensities, i.e. amounts of driving rain water onto
the building envelope per time interval. The empirical model is
useful for analyses of our full-scale measurements. For both models
we concentrated on the second step (from site to building façade)
of the general two-step approach (figure 1.1).
The objectives of the experiments were (a) the development and testing
of driving rain gauges, and (b) the acquisition of driving rain data
simultaneously with relevant weather data (in real circumstances, in
full scale). The measured data should also be suited for the
validation of CFD simulations of wind and driving rain in the
same situation.
We chose the Main Building of the TUE mainly because of the relative
simplicity of its geometry and the site topography. This simplicity
relates to the following aspects. The Main Building is obviously
higher than nearby buildings. Its height surpasses 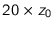 . Its
wind field is hardly affected by other buildings and obstacles for
south-west to west winds. Another important aspect is that a suitable
location for site reference measurements of wind and rain was easily
defined at the west side of the Main Building. Moreover, the large
west façade is oriented towards the prevailing direction for wind
and rain.
. Its
wind field is hardly affected by other buildings and obstacles for
south-west to west winds. Another important aspect is that a suitable
location for site reference measurements of wind and rain was easily
defined at the west side of the Main Building. Moreover, the large
west façade is oriented towards the prevailing direction for wind
and rain.
The instrumentation is described extensively in section
3.2. Recommendations, which do not relate to
the driving rain gauges, are:
-
- The output of the disdrometer used by us has two
disadvantages for our purposes. Firstly, the disdrometer
gives the raindrop number concentration spectrum, which
is derived from the quantity which we are interested in,
namely the raindrop mass flux spectrum. Secondly, the
interval of the size classes increases with the
diameter, which results in larger absolute errors of the
real mass flux at larger diameters. The two
disadvantages can be solved by outputting every detected
raindrop with its diameter and velocity. It is
recommended to adapt the software of the disdrometer in
this way.
-
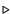
- The two-dimensional video-disdrometer of
[Schönhuber et al. 1994] is able to register details
of raindrops. It could be used to verify actual raindrop
spectra with those measured by the optical disdrometer
of [Löffler-Mang and Joss 2000] which we used.
The video-disdrometer can also be mounted in a
façade in order to validate simulated catch ratios
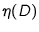 (eq. 2.26) directly from
measurements of
(eq. 2.26) directly from
measurements of
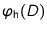 and
and
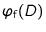 .
.
-
- The measurement set-up at the TUE site may be continued and
extended with instruments for the measurement of outdoor
air temperature, relative humidity, solar irradiation
etc., so that every important climatological parameter can
be included to the benefit of heat-air-moisture studies.
The conclusions of the international full-scale driving rain gauge
comparison test are listed in section 4.4 (and were
partially presented in [Högberg et al. 1999]).
Adding some suggestions, we repeat the most important conclusions
here:
- The experiments resulted in the formulation of design rules for
driving rain gauges. These design rules relate to the catchment
area, the prevention of drops from remaining stuck on the
surface of the driving rain collector, the temporal resolution
of the water flux gauge and the finish of the collector surface.
- The TUE-II gauge, which was developed at the TUE and is
equipped with a rotating wiper (figure 3.14), accurately
registers driving rain intensities. It has a good resolution
for shorter time intervals (0.001 mm h
 for 10-min
periods). Its wiper keeps the surface clean and forces impinged
raindrops to coagulate and drip down (hence less
evaporation). Moreover, it is not sensitive to wind.
for 10-min
periods). Its wiper keeps the surface clean and forces impinged
raindrops to coagulate and drip down (hence less
evaporation). Moreover, it is not sensitive to wind.
- The TUE-I gauge, which is similar to TUE-II except
that it is not equipped with a rotating wiper (figure
3.13), registers approximately half of the monthly
driving rain amount measured by the TUE-II gauge (table
4.1). This is also valid for 10-min periods (figure
4.1c).
- The monthly driving rain amounts of the CTH, DTU and TUE-II
gauges deviate within 30% from each other (table
4.1). On much smaller time bases, such as 10-min
intervals, gauge responses can deviate significantly (figures
4.1-4.4). This applies
especially for small time bases of the used tipping-bucket
driving rain gauge (CTH): during a 10 min period it tips only
once at a driving rain intensity of 0.18 mm h
 .
.
-
- Given the results of the CTH gauge for driving rain
measurements, we suggest that for short-time intervals (like 5-
or 10-min intervals) one should apply a continuous measuring
principle instead of the tipping-bucket principle.
Indeed, given the necessary yet cumbersome correction of the
tipping-bucket gauge data (sections
3.4.3 and
5.1), the suggestion also
applies to horizontal rain measurements.
- The effect of size and shape of the catchment area cannot
clearly be deduced from the experiments. A comparison of the CTH
gauge (0.032 m
 ) and the TUE-I gauge (0.5 m
) and the TUE-I gauge (0.5 m ) does
not give a straightforward conclusion, because of the
differences in measuring principle.
) does
not give a straightforward conclusion, because of the
differences in measuring principle.
-
- It is recommended for further research to compare simultaneously
the readings of driving rain gauges with different catchment
areas but with the same continuous measuring principle. One
could, for instance, add the CTH gauge and the TUE-II
gauges as references. Further measurements with the disdrometer
(with which we measured during a too short period) may be useful
for explaining the differences between the readings of driving
rain gauges.
Another line of research are calculations with a model for
raindrops sticking, coagulating and running off on a driving
rain collector, as mentioned in [Blocken et al. 2001].
- Lower driving rain intensities (measured with the TUE-II
gauge) are overestimated by the DTU gauge (figures
4.1b-4.4b). The scatter in
the DTU/TUE-II correlations is larger than in the
TUE-I/TUE-II correlations. This is probably due to the
noise caused by the wind acting on the freely suspended
collector. The applied signal-processing method (see section
3.4.6) was kept
simple and (
 ) can perhaps be improved.
) can perhaps be improved.
-
- The possibility of splashing and the effects of protruding rims
and other projections were not investigated. With our full-scale
measurement set-up, it is possible to mount at least three
gauges with different protruding rims at P4/5/7. An
investigation on splashing effects is less easy; perhaps one may
use video cameras.
-
- As it occurred that the reservoirs of the TUE-II and
TUE-I gauges overflowed during heavy driving rain, it is
recommended to investigate other types of continuous water flux
measurements. We have done some laboratory experiments with a
drop-counting device [Bijsterbosch 2000]. Combined with a
collector of
 m
m , it has a resolution
of 0.0006 mm h
, it has a resolution
of 0.0006 mm h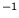 for 10-min periods and an accuracy of
approximately 5% for driving rain intensities ranging at
least from 0.12 to 1.20 mm h
for 10-min periods and an accuracy of
approximately 5% for driving rain intensities ranging at
least from 0.12 to 1.20 mm h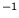 (one drop equals 0.05 g
(one drop equals 0.05 g
 5%). We recommend to test it in full scale first.
5%). We recommend to test it in full scale first.
The full-scale experiments at the TUE site resulted in a unique series
of continuous measurements during 24 months of driving rain on the
west façade of the Main Building and wind and rain at the
well-defined site reference location. Raindrop spectra with a
disdrometer were measured during 3 months too. The measurements are
detailed (data at 5-minute intervals were provided) and are available
for future research (at the website http://sts.bwk.tue.nl/drivingrain/).
Section 5.4 gives a summary of the
measurement results. The present study introduces the following new
items to our knowledge on driving rain:
- -
- a time series of detailed measurements of driving rain on a
façade on a particular building in an urban surrounding
with well-defined site reference measurements,
- -
- the readings of different types of driving rain gauges were
compared with each other in a full-scale comparison test
(see chapter 4),
- -
- raindrop spectra were measured with a disdrometer of
[Löffler-Mang and Joss 2000]. Unfortunately, the number of
measured spectra during driving rain was rather small.
-
- Further raindrop spectrum measurements are
recommanded, because we could not conclude our
investigation on the influence of raindrop spectrum on
driving rain quantities,
- -
- driving rain intensities vary much at a façade position and
on small time-scales (5 min), even for narrow ranges of
reference wind speed, wind direction and horizontal
rain intensity (see e.g. figure 5.14 and
section 5.2.5).
Moreover, the correlation between the two measurement
positions P4/5 and P6 is very complex and depends to a
great degree on wind direction (section
5.2.6),
- -
- the traditional empirical model (model 1, eq. 5.3),
based on [Lacy 1965] and implemented in the British
Standard 8401 [BSI 1992], is improved by taking the wind
direction and the position on the façade more explicitly
into account (model 2, eq. 5.4).
Model 1 yields less realistic estimates of (especially
maxima of) 5-min driving rain intensities than model 2.
However, the models overestimate the cumulative
driving rain amounts after 24 months by up to 35-45%.
-
- In order to validate models 1 and 2 further,
we recommend measurements of the distribution
of driving rain intensity over the façade
on more than two façade
positions. Probably a better line of research
are driving rain measurements on other
buildings; below we will suggest some
conditions for such experiments.
We investigated a large part of the two-step approach (figure
1.1) in chapter 5, but we
did not show every possible analysis of the measurement data, such as:
-
- an investigation on the relation between hourly values and 5-min
(10-min) values, as generally only hourly values of measured
wind and rain parameters are available at a weather station,
-
- an analysis of the temporal development of horizontal and
driving rain intensities during rain spells.
Section 6.5 summarises our CFD simulations of wind
and driving rain at the TUE site. Figures
6.16 to
6.19 depict the results of
simulated driving rain intensity distributions over the west
façade of the Main Building. The main conclusions are:
- In spite of the known limitations of the applied
 -
-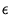 model (e.g. [Murakami et al. 1992]), the
practically limited number of grid cells and the use of a
structured grid with inevitably non-ideally shaped grid
cells, the simulated wind speed at the façade is within
the standard deviation of the full-scale wind speed
measurements at position P4.
Simulated mean pressure coefficients over the west
façade compare quite well with wind tunnel and
full-scale measurements of [Geurts 1997].
model (e.g. [Murakami et al. 1992]), the
practically limited number of grid cells and the use of a
structured grid with inevitably non-ideally shaped grid
cells, the simulated wind speed at the façade is within
the standard deviation of the full-scale wind speed
measurements at position P4.
Simulated mean pressure coefficients over the west
façade compare quite well with wind tunnel and
full-scale measurements of [Geurts 1997].
- Catch ratios
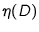 calculated with turbulent drop dispersion
have higher values than without turbulent drop dispersion.
Due to the (extra) turbulent velocity component, drops are more
easily driven towards the façade when they come close to it.
The smaller the drops are, the easier they are driven onto
the façade. Moreover, the longer a drop flies closely to a
façade, the higher is the probability that it is driven onto
the façade.
Figure 6.3 illustrates drop
trajectories resulting from the two drop trajectory models;
figures 6.10 to
6.14 show simulated catch ratios
calculated with turbulent drop dispersion
have higher values than without turbulent drop dispersion.
Due to the (extra) turbulent velocity component, drops are more
easily driven towards the façade when they come close to it.
The smaller the drops are, the easier they are driven onto
the façade. Moreover, the longer a drop flies closely to a
façade, the higher is the probability that it is driven onto
the façade.
Figure 6.3 illustrates drop
trajectories resulting from the two drop trajectory models;
figures 6.10 to
6.14 show simulated catch ratios
 .
.
- A comparison between the measurements and the simulations
(based on the raindrop spectrum parameterisation of
[Wessels 1972]) reveals that the results calculated
with turbulent drop dispersion are likely to overestimate
the measured driving rain intensities. The results
calculated without turbulent drop dispersion are likely to
underestimate the measurements.
-
- To validate our CFD driving rain simulations more
precisely, it is needed to measure wind speed and driving
rain intensities at more positions close to and on the
façade.
- As concluded before, the measured driving rain
intensities for a given façade section, reference wind
speed and wind direction show large variations. The
driving rain intensities simulated without turbulent
drop dispersion and based on the raindrop spectrum
parameterisation of
[Wessels 1972], yield an almost linear relation with
horizontal rain intensity:
 , where
, where 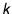 depends only on the shape (in our
case, parameter
depends only on the shape (in our
case, parameter 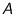 ) of the raindrop spectrum. However,
when measured raindrop spectra are used in the
simulations, these simulated driving rain intensities show
scatter too. Because the number of measured raindrop
spectra during driving rain is rather small, we can not
yet decisively conclude whether the relation
) of the raindrop spectrum. However,
when measured raindrop spectra are used in the
simulations, these simulated driving rain intensities show
scatter too. Because the number of measured raindrop
spectra during driving rain is rather small, we can not
yet decisively conclude whether the relation
 is actually valid.
is actually valid.
-
- It is therefore recommended to elaborate the problem of
the previous item with more measurements of raindrop
spectra and driving rain.
- Altogether, the following aspects for reliable CFD
results of wind and driving rain are important:
- -
- experience with the CFD program, useful
references, like [Bottema 1993a], and
validations of simulated data with measured
data will make one conscious about the
possibilities and limitations of the applied
models. Standards on CFD simulations of
wind nearby buildings are still in
development though,
- -
- the building geometry and the surrounding
topography should be simple enough for
CFD modelling. An important condition for
the surrounding topography is the presence
of a site reference location and an
unobstructed fetch for a certain range of
wind directions. These will determine the
values of the displacement height
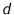 and
the roughness length
and
the roughness length  . The larger
region around the site should also be
considered for these parameters. Preferably,
the considered building has distinct
dimensions compared to its surroundings
(e.g.
. The larger
region around the site should also be
considered for these parameters. Preferably,
the considered building has distinct
dimensions compared to its surroundings
(e.g.
 ),
),
- -
- the grid and the size of the computational
domain depend on the expected wind flow and
raindrop trajectories. For instance, the
stopping distance of the smallest considered
raindrop determines the grid size nearby the
building envelope,
- -
- the modelling of turbulent drop dispersion is
still an issue for research,
- -
- reliable results depend on realistic values
of climatological parameters, namely wind
speeds, wind directions, horizontal rain
intensities and raindrop spectra. For a
climate like that of the Netherlands, the
raindrop spectrum parameterisations of
[Wessels 1972] are very useful.
In most of the previous suggestions we addressed further studies
for our own site.
More general suggestions are formulated in the following items:
-
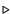
- From the start of the present study in 1996, only few
comparisons between full-scale measurements and
simulations of driving rain on a particular building in
a particular topography have been reported
([van Mook 1999a] and
[Blocken et al. 2001]). However, the number of
studies on CFD simulations without the validation
with full-scale measurements is larger (section
1.3).
Important for the advance of the knowledge on driving
rain are several further studies in which CFD
simulations are validated with full-scale measurements.
Of course, one should carefully select another situation
(i.e. a particular building and its environment), given
the limitations of CFD simulations. One should also
pay attention to the instrumentation and the measurement
method. In order to make a comparison between our
situation and other situations feasible, we recommend to
carry out measurements and simulations in situations
which are comparable to our situation. This means:
- -
- The geometry of buildings is considered
comparable if it has a simple shape, i.e.
without many or complex protrusions or
recesses. Given the Main Building, it
would be interesting to investigate e.g.
two-dimensional situations of two blocks
of flats or two rows of terraced houses,
and three-dimensional situations of a
tower, a building with a large indentation
in the middle of the roof or a building
with a large canopy.
With regard to the surrounding topography
we refer to our above-mentioned
considerations for reliable CFD
results.
- -
- The climate of the site is nearly the same
as that at the TUE site, as the driving
rain onslaught in moderate maritime
climates are very different from the
onslaught in e.g. tropical thunderstorms
(cf. [Choi 1999a]).
- -
- A full-scale experiment is designed with
the approach described in chapters
3 and
4 and with
the recommendations resulting from these
chapters borne in mind. We recommend
especially to obtain measured data at
small time bases (of the order of 1-5
min), to measure continuously during at
least 6 months, not to use tipping-bucket
gauges, to measure raindrop spectra, and
--of course-- to use a driving rain
gauge as accurate as TUE-II.
The comparison between our situation and other
situations may relate to: the validation of model 1 (eq.
5.3) and model 2 (eq. 5.4),
the validation of the turbulent raindrop dispersion
modelling in CFD and the influence of raindrop
spectra on driving rain.
-
- Within the context of the previous item, collaboration
between driving rain research projects at different
locations, like by [Blocken et al. 2001], should be
stimulated.
-
- Pictures of façades which were just exposed to driving
rain, may give a nice overview on the wetting of a
façade, and help in acquiring qualitative data for
validation of CFD simulations. Such pictures may also
serve to understand the influence of façade details
(e.g. projections) on driving rain onslaught and
run-off. Moreover, small projections and canopies are
difficult to implement in a CFD model. It is
recommended to take photographs (before, during and
after rain), such as done by [El-Shimi
et al. 1980]
and [Snape and
Atkinson 1999].
-
- The TUE-II gauges were suitable for our driving rain
measurements, but they are not easily installed due to
the size of their collectors and the space needed for
the reservoirs and balances. A `portable' gauge is
needed when one would like to do more in situ driving
rain measurements. Perhaps a driving rain gauge equipped
with a drop-counting device (see above) could serve for
this.
Subsections
© 2002 Fabien J.R. van Mook
ISBN 90-6814-569-X
Published as issue 69 in the Bouwstenen series of the Faculty of Architecture, Planning and Building of the Eindhoven University of Technology.
![]() ) and gives suggestions for further
research (indicated by
) and gives suggestions for further
research (indicated by
![]() ).
).
![]() . Its
wind field is hardly affected by other buildings and obstacles for
south-west to west winds. Another important aspect is that a suitable
location for site reference measurements of wind and rain was easily
defined at the west side of the Main Building. Moreover, the large
west façade is oriented towards the prevailing direction for wind
and rain.
. Its
wind field is hardly affected by other buildings and obstacles for
south-west to west winds. Another important aspect is that a suitable
location for site reference measurements of wind and rain was easily
defined at the west side of the Main Building. Moreover, the large
west façade is oriented towards the prevailing direction for wind
and rain.
![]() (eq. 2.26) directly from
measurements of
(eq. 2.26) directly from
measurements of
![]() and
and
![]() .
.