2.3 Driving rain

Generally one considers ``driving rain'' as rain that is carried (driven) by wind. A synonym is ``wind-driven rain''. Here, we will use a more restricted definition: driving rain (or wind-driven rain) is rain that is carried by wind and driven onto building envelopes. Usually we will look at building envelopes which are vertical, although rain distribution on roofs is affected by wind too.

Because wind always plays a role in formation and distribution of rain, the quantities and physical concepts described in the previous section 2.2 also apply for driving rain (yet sometimes slightly adapted).

2.3.1 Theoretical model

The general model of driving rain used in this study takes the trajectories of raindrops into account. In reality, every individual drop has its individual drop trajectory. Moreover, the lifetime of a drop is affected by drop interaction (collision and breakup) and the environment (wind and evaporation). The model takes only the influence of the wind into account. This is sketched in figure 2.12 for raindrops of one particular size. From the discussion in section 2.2.3 we expect that the trajectories of raindrops will also be affected by the turbulence in the wind. The turbulent dispersion of raindrops will imply that raindrops starting at the same point will follow different paths (figure 2.12).

Figure 2.12: Sketch of trajectories of raindrops with the same diameter. The wind is from left to right. The trajectories disperse due to the turbulence of the wind.

The driving rain amount per drop size in relation to the reference rain amount per drop size is characterised by a catch ratio $\eta (D)$:

$$\eta(D) = \frac{\varphi_{\text{f}}(D)}{\varphi_{\text{h}}(D)},$$ (2.26)

with $\varphi_{\text{f}}(D)$ = the raindrop mass flux spectrum on the façade surface, and $\varphi _{\text {h}}(D)$ = the raindrop mass flux spectrum through the horizontal in the undisturbed wind flow (calculated using eq. 2.16).

The reference of $\varphi_{\text{f}}(D)$ in eq. 2.26 is taken in the wind flow undisturbed by individual buildings or other obstacles. The reference is preferably taken at the site itself and then the model applies for the second step in our general two-step approach (figure 1.1).

The driving rain intensity $R_{\text {f}}$ on the building envelope is:

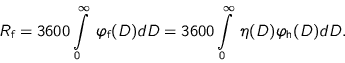$$R_{\text{f}} = 3600 \int\limits_{0}^{\infty} \; \varphi_{\t... ...\int\limits_{0}^{\infty} \; \eta(D) \varphi_{\text{h}}(D) dD.$$ (2.27)

The catch ratio $\eta (D)$ (and eventually the driving rain intensity) depends on the following factors:

• raindrop size --the driving rain intensity depends on the raindrop spectrum,
• wind field,
• building geometry and topology of the surroundings,
• position on the building envelope.

The model can be elaborated into a numerical model. This will be done in chapter 6 (CFD simulations). Similar numerical models were described in the literature, e.g.: [Bookelmann and Wisse 1992], [Choi 1993], [Karagiozis and Hadjisophocleous 1996], [van Mook et al. 1997], [Sankaran and Paterson 1995a], [Hangan and Surry 1998] and [Blocken and Carmeliet 2000a]. However, the cited authors (except for [Sankaran and Paterson 1995a]) did not take the turbulent dispersion of raindrops into account: the trajectories were calculated according to the mean wind field. In chapter 6 we will study the differences resulting from calculations with or without turbulent drop dispersion.

2.3.2 Empirical model

In the practice of driving rain measurements, raindrop spectra have never been measured, and raindrop trajectories are not determined. Based on the integral rain quantities, one correlates the driving rain intensity with the horizontal rain intensity, i.e. the reference in the undisturbed wind flow, by means of their ratio:

$$k = \frac{R_{\text{f}}}{R_{\text{h}}}.$$ (2.28)

$k$ is here called ``driving rain ratio''. Measured values of $k$ can be found e.g. in [Hens and Mohamed 1994], [Osmond 1996] and [Kragh 1998].

1. Vertical rain intensity Some authors try to distinguish several factors in the driving rain ratio. The first step is to define a vertical rain intensity $R_{\text{v}}$ [mm h$^{-1}$], i.e. the rain intensity through a vertical plane in the undisturbed wind flow. It is assumed to be related to the reference wind speed and horizontal rain intensity in the following way:

$$R_{\text{v}} = \alpha \: U_{\text{r}} \; R_{\text{h}}^\beta,$$ (2.29)

with $U_{\text{r}}$ = the reference wind speed [m s$^{-1}$], and $\alpha$ and $\beta$ are empirical constants.

[Lacy 1965] calculated $\alpha$ and $\beta$ as follows: he assumed that the ratio of vertical and horizontal rain intensities is equal to the ratio of wind speed and terminal velocity of drops of median size ($D_{50}$):

$$R_{\text{v}} = R_{\text{h}} \frac{U_{\text{r}}}{w_{\text{term}}(D_{50})}.$$ (2.30)

He gives an empirical relationship between $R_{\text {h}}$ and $D_{50}$ which he deducted from data presented by [Laws and Parsons 1943]:

$$D_{50} = 1.238 R_{\text{h}}^{0.182},$$ (2.31)

and by combining this with the $w_{\text{term}}(D)$ relation deduced from [Best 1950] he obtains:

$$w_{\text{term}}(D_{50}) = 4.505 R_{\text{h}}^{0.123}.$$ (2.32)

Substituting eq. 2.32 in eq. 2.30 yields the desired relation:

$$R_{\text{v}} = 0.222 \; U_{\text{r}} \; R_{\text{h}}^{0.88},$$ (2.33)

so that $\alpha$ = 0.222 and $\beta$ = 0.88.

[Lacy 1965] showed also that calculated values of $R_{\text{v}}$ (eq. 2.33) agree quite well with measurements of $R_{\text{v}}$ for 75 storms with driving rain that occurred during 1948-1963 in Garston (UK). Only rain storms of more than 10 hours were taken into account; the time interval of the measurements was not specified. Measurements of [Künzel 1994] at Holtzkirchen (DE) yielded a value for $\alpha$ of about 0.2.

Figure 2.13: Lacy's parameter $\alpha$ (with $\beta = 0.88$) as function of horizontal rain intensity, for raindrop spectra of [Marshall and Palmer 1948] ( $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$), and [Ulbrich 1983] ( $\includegraphics[width=2em]{gen/m-stippel.eps}$: $\mu = -1$, $\includegraphics[width=2em]{gen/m-streep.eps}$: $\mu = 1$, $\includegraphics[width=2em]{gen/m-streep-stippel.eps}$: $\mu = 2$). Cf. figure 2.10.

Figure 2.14: Lacy's parameter $\alpha$ (with $\beta = 0.88$) as function of horizontal rain intensity, for raindrop spectra of [Best 1950]. $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$: $A=1.30$, $a=0.232$, $b=2.25$, $C=67$, $q=0.846$. Variation of $\alpha$ calculated from the measurements of [Wessels 1972]: $\includegraphics[width=2em]{gen/m-stippel.eps}$: $A=0.88$, $a=0.21$, $\includegraphics[width=2em]{gen/m-streep.eps}$: $A=1.77$, $a=0.21$. Cf. figure 2.11.

With the quantities defined in section 2.2.4, one can express the vertical rain intensity $R_{\text{v}}$ [mm h$^{-1}$] in terms of the reference wind speed $U_{\text{r}}$ [m s$^{-1}$] and the integral of the raindrop mass concentration spectrum (i.e. the liquid water content $W$ [kg m$^{-3}$]):

$$R_{\text{v}} = 3600 \; U_{\text{r}} \; \int\limits_{0}^{\infty} m(D) dD = 3600 \; U_{\text{r}} \; W.$$ (2.34)

To investigate the validity of the model of Lacy (eq. 2.29) for several given raindrop spectra, we combine equations 2.29 and 2.34, yielding $3600 U_{\text{r}} W = \alpha U_{\text{r}} R_{\text{h}}^\beta$, and plot $\alpha = 3600 W / R_{\text{h}}^\beta$ for $\beta = 0.88$. Figure 2.13 shows this plot for raindrop spectra of [Marshall and Palmer 1948] and [Ulbrich 1983] (compare with figure 2.10). In figure 2.14 $\alpha$ is plotted for Best spectra according to parameters given by [Best 1950] and according to the measurements in the Netherlands of [Wessels 1972] (cf. figure 2.11). These figures show that parameter $\alpha$ becomes constant for larger $R_{\text {h}}$, but for rain intensities below 1 mm h$^{-1}$ $\alpha$ can increase up to 0.4. Moreover, rainfall with larger drops will yield a lower value of $\alpha$. Applying the data of [Wessels 1972], we find that $\alpha$ ranges from 0.2 to 0.35. The generally measured value 0.22 (i.e. at the lower part of the mentioned range) might originate from the sensitivity of free-standing driving rain gauges, which is often low for low rain intensities and for rainfall with mainly small drops.

2. Driving rain intensity The second step is to relate vertical rain intensity to driving rain intensity:

$$R_{\text{f}} = \kappa \; R_{\text{v}}.$$ (2.35)

The obstruction factor $\kappa$ is meant to reflect the building geometry, surrounding topology and façade position. It ranges from 0.1 to 2. Examples for values of $\kappa$ are found in [Lacy 1965], [Frank 1973], [Lacy 1977], [Brown 1988], [Henriques 1992] and [Künzel 1994].

Finally, we conclude that both the coefficient $\alpha$ and the obstruction factor $\kappa$ depend on the raindrop spectrum. So, they are interdependent. It is probably better to merge the two coefficients into one coefficient ( $\kappa\times\alpha$).