5.2 General presentation of the measured data

In the previous section 5.1, the data (sub)set of the full-scale measurements at the TUE site was defined by specifying the clock period and the quantities of interest. In this section, this data set, along with weather data from the weather station at Eindhoven Airport, is presented.

5.2.1 Wind

Figure 5.2: Monthly mean wind speeds at Eindhoven Airport (30-year normal: $\includegraphics[width=0.5em]{gen/m-rondje.eps}$, measured [KNMI 1997-99]: $\includegraphics[width=2em]{gen/m-streep.eps}$) and at the Auditorium (based on 5-min averages: $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$). Period: 1-12-1997 to 30-11-1999. An asterisk indicates that the monthly percentage of available clock periods at the TUE site is below 80%.

Figure 5.2 shows monthly wind speed averages obtained from measurements at the Auditorium and at the meteorological station at Eindhoven Airport. For the airport wind speeds, 30-year normals and the actual monthly averages were obtained from [KNMI 1997-99]. The figure also shows the averaged wind speed on top of the mast on the Auditorium. These data are based on 5-min averages, and only wind speeds of 0.1 m s$^{-1}$ or more were taken into account. An asterisk in the graph indicates that the monthly percentage of available clock periods is below 80%. Inspection of figure 5.2 reveals that the actual monthly averages of wind speeds at Eindhoven Airport and at the Auditorium are very similar; both data sets have generally lower wind speeds than the 30-year normals. Since a comparison of hourly averages is more informative than monthly averages, this will be the subject of the following part of this section 5.2.1.

Figure 5.3: Correlations of hourly horizontal wind speeds at Eindhoven Airport (EA) [KNMI 2000] and the Auditorium (P1), for four wind directions $\Phi _{\text {EA}}$. Period: 1-12-1997 to 30-11-1999.

Figure 5.3 shows correlations of hourly wind speeds at Eindhoven Airport $U_{\text{h,EA}}$ and the Auditorium $U_{\text{h,\texttt{P1}}}$, selected for four wind direction intervals at Eindhoven Airport ( $\Phi _{\text {EA}}$). The data for Eindhoven Airport, published in [KNMI 2000], consists of hourly wind speeds and hourly wind directions. The wind speeds published were obtained by rounding off to 0.5 m s$^{-1}$ and subsequently by the exposure correction to obtain $U_{\text {h}}$ at 10 m height on a terrain with $z_0=0.03$ m ([Wieringa 1996] and [Verkaik 2000]). This explains the vertical alignment of the measurement points in figure 5.3. Only wind data with $U_{\text{h,EA}}\ge0.5$ m s$^{-1}$ are taken into account. The data of the Auditorium are simply based on our measurements (uncorrected wind speeds). The correlations in figures 5.3a, c and d (i.e. for wind from the north, south and west) are similar: $U_{\text{h,\texttt{P1}}}/U_{\text{h,EA}}=0.90$. This value is lower than the value of 1.13 reported by [Geurts 1997]. He used 30-min averages of the wind speeds which he measured at the Auditorium during wind exceeding a predefined speed (5-8 m s$^{-1}$) and he used wind speed averages of the last 10 min of every clock hour at the Airport. This difference between his and our data processing may explain the difference in the values of $U_{\text{h,\texttt{P1}}}/U_{\text{h,EA}}$. The statistics of this correlation is discussed in more detail by [de Wit et al. 2002].

The correlation $U_{\text{h,\texttt{P1}}}/U_{\text{h,EA}}$ for eastern wind is smaller (0.48, figure 5.3b). This is most likely due to the position of the measurement point at the Auditorium (P1), which is located west of the Main Building. The anemometer at P1 is measuring in the wake of the Main Building when wind is blowing from the east. In the case of eastern wind, there is also an influence of the town on the wind measurements at Eindhoven Airport (located west of the town). However, the airport data were already corrected to compensate for such influences.

Figure 5.4: Cumulative relative distribution of wind speeds $U_{\text {h}}$. Based on 5-min data measured at the Auditorium from 1-12-1997 to 30-11-1999. Mean and median 5-min wind speeds are also indicated.

Finally, for illustrative purposes, the cumulative relative number distribution of the 5-min wind speeds at the Auditorium is depicted in figure 5.4. The mean wind speed for the whole 24 month period is 4.0 m s$^{-1}$ (the standard deviation equals 1.9 m s$^{-1}$).

5.2.2 Horizontal rain amounts and intensities

Table 5.2: Monthly horizontal precipitation amounts [mm] at positions P2 and P3 at the Auditorium, at Eindhoven Airport (EA) [KNMI 1997-99], and monthly driving rain amounts at P4/5 and P6 (TUE-II type gauges in both cases). Asterisks indicate that the monthly percentage of available clock periods of the TUE data is below 80%.

	horizontal rain amounts			dr. r. amounts
year month	P2	P3	EA	P4/5	P6
1997 12	64.5	57.8	53.1	2.78	--
1998 01	67.7	62.8	58.2	5.77	--
1998 02	12.9	11.8	10.8	0.83	--
1998 03	85.2	76.3	80.3	4.87	5.25
1998 04 $\ast$	77.6	74.4	74.7	1.11	2.46
1998 05	32.5	21.5	26.5	0.94	2.03
1998 06 $\ast$	64.5	63.9	148.2	3.92	8.38
1998 07	56.2	54.8	50.3	1.93	2.75
1998 08	48.3	47.1	47.8	3.35	5.36
1998 09	131.8	132.6	167.7	9.61	14.21
1998 10	143.2	138.7	158.5	11.70	13.36
1998 11	80.1	75.4	80.4	0.59	1.17
1998 12	57.2	50.1	51.7	3.43	5.07
1999 01	85.8	79.1	102.6	3.30	6.20
1999 02	65.7	56.8	71.0	4.06	10.21
1999 03	73.1	66.4	68.2	4.31	5.74
1999 04	38.4	36.2	41.5	1.49	2.51
1999 05	53.4	52.8	71.6	0.12	0.52
1999 06	63.4	60.6	53.8	2.43	3.10
1999 07	46.9	44.2	68.8	2.25	4.54
1999 08	95.8	89.6	92.1	1.70	2.44
1999 09	29.8	25.6	38.0	0.76	1.23
1999 10	28.2	27.5	27.5	0.82	1.86
1999 11	34.2	35.6	43.2	0.80	1.72
totals	1536.6	1441.7	1686.5	72.90	100.13

Table 5.2 lists monthly precipitation amounts measured at Eindhoven Airport [KNMI 1997-99] and at the Auditorium. One should bear in mind that the precipitation data include rain, snow and other types of precipitation. However, according to the monthly weather reports [KNMI 1997-99], the monthly number of days with snowfall was approximately normal. (Normally, snow occurs during the months of November to April and the largest number of monthly snow days (8) occurs in February.) So, the monthly precipitation heights are often close to the actual rain amounts. Thirty-year normals of monthly rain amounts at Eindhoven Airport are not presented in the table, because the meteorological institute did not yet publish them. An asterisk in table 5.2 indicates that the number of available clock periods of the TUE data is below 80%. We recall here that horizontal rain is measured at two positions on the roof of the Auditorium, namely P2 and P3 (figure 3.4). Figure 5.5 depicts the monthly rain amounts measured at Eindhoven Airport and at position P2 on the Auditorium.

Figure 5.5: Monthly precipitation heights at Eindhoven Airport (measured [KNMI 1997-99]: $\includegraphics[width=2em]{gen/m-streep.eps}$) and at the Auditorium (at position P2, based on 5-min clock periods: $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$). Period: 1-12-1997 to 30-11-1999. Asterisks indicate that the monthly percentage of available clock periods of the TUE data is below 80%.

Striking in the table and figure are the very large rain amounts measured in June, September and October 1998. Unfortunately, due to a 2-day malfunction of the data acquisition system in June 1998, a large amount of rain was not registered at the Auditorium. The high rainfall during September and October 1998 is considered in section 5.2.7, along with the corresponding wind and driving rain data. In general, the rain amounts measured at Eindhoven Airport and the Auditorium are in good agreement. There is no reason to consider systematic deviations due to topography, because the distance between these two measurement sites is not very large and the exposure of both sites is very open.

Table 5.3: Horizontal rain amounts at positions P2 and P3 at the Auditorium and driving rain amounts at P4/5 and P6 for twelve wind direction intervals. The last two columns show respectively the percentage of all available 5-min periods per wind direction interval and the percentage of only those available clock periods with rain at P2 or P3. Clock periods with $U_{\text {h}}<0.3$ m s$^{-1}$ are listed separately. Based on 5-min data from 1-12-1997 to 30-11-1999.

	horizontal rain				driving rain				number
$\Phi$ $\pm$ 15$^\circ$	P2		P3		P4/5		P6		all	rain
	[mm]	[%]	[mm]	[%]	[mm]	[%]	[mm]	[%]	[%]	[%]
0$^\circ$	49.9	3	47.5	3	0.01	0	0.06	0	5	2
30$^\circ$	38.2	2	37.4	3	0.00	0	0.00	0	7	1
60$^\circ$	20.0	1	18.8	1	0.00	0	0.00	0	7	2
90$^\circ$	13.2	1	12.9	1	0.00	0	0.00	0	3	1
120$^\circ$	51.5	3	50.7	4	0.00	0	0.00	0	5	3
150$^\circ$	73.9	5	71.3	5	0.00	0	0.00	0	4	5
180$^\circ$	157.4	10	154.2	11	0.11	0	0.11	0	10	12
210$^\circ$	403.6	26	363.9	25	11.47	16	8.31	8	21	30
240$^\circ$	311.3	20	289.8	20	24.22	33	23.41	23	18	21
270$^\circ$	229.3	15	212.5	15	29.04	40	44.83	45	10	13
300$^\circ$	108.1	7	103.8	7	6.16	8	17.24	17	6	6
330$^\circ$	77.5	5	76.1	5	1.86	3	6.15	6	4	4
$U_{\text {h}}<0.3$
m s$^{-1}$	2.8	0	2.7	0	0.02	0	0.02	0	0	0
totals	1536.6	100	1441.7	100	72.90	100	100.13	100	100	100

The distribution of 5-min horizontal rain amounts over twelve wind direction intervals is listed in table 5.3. Clock periods with $U_{\text {h}}<0.3$ m s$^{-1}$ are listed separately. Obviously, most rain is coming with wind from the south-west ($\Phi\approx$ 225$^\circ$). The horizontal rain amount for wind directions 195$^\circ$-255$^\circ$ is approximately 45% of the total rain amount over all wind directions, and occurs during approximately 50% of the total 5-min clock periods with rain. So, the average rain intensity for wind directions 195$^\circ$-255$^\circ$ is only slightly lower than the rain intensity averaged over all wind directions. On the other hand, the average rain intensity for wind directions 15$^\circ$-115$^\circ$ is almost equal to the overall average rain intensity.

Figure 5.6: Cumulative relative distributions of horizontal rain intensities, in terms of the number of 5-min clock periods with that intensity ( $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$) and the horizontal rain amount ( $\includegraphics[width=2em]{gen/m-streep.eps}$). Based on 5-min data measured at position P2 from 1-12-1997 to 30-11-1999. The median 5-min horizontal rain intensity (according to rain amounts) is also indicated.

Figure 5.6 shows two distributions of horizontal rain intensities measured at the Auditorium during the 24-month measuring period. One distribution (the solid line) is the cumulative relative distribution of the number of 5-min clock periods with a particular rain intensity. The other distribution (the dashed line in the figure) is the cumulative relative distribution of the rain amount contributed by all clock periods with a particular rain intensity. The dashed line increases less with the horizontal rain intensity than the solid line, because there are less clock periods with a high rain intensity than with a low rain intensity and because clock periods with a high rain intensity contribute more to the total rain amount than clock periods with a low rain intensity. The cumulative relative distribution in terms of the rain amount (dashed line) is hence more useful. The median indicated in the figure represents the rain intensity below which half of all rain water is collected. At position P2 on the Auditorium the median 5-min rain intensity is 2.2 mm h$^{-1}$.

Figure 5.7: Relative number distribution of daily amounts of horizontal rain, measured at the Auditorium (P2) for the winter months December 1997 to February 1998 and December 1998 to February 1999 ( $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$), and measured at De Bilt [Buishand and Velds 1980, p. 93] for the winters (December-February) from 1906 to 1977 ( $\includegraphics[width=2em]{gen/m-stippel.eps}$). The most right bar denotes daily amounts of 10 mm and more. The most left bar of the solid line denotes zero daily amounts.

Figure 5.7 shows the relative number distribution of daily amounts of horizontal rain at De Bilt presented by []p. 93]buishand:1980, and at the Auditorium (P2). The data of De Bilt were taken from winters from 1906 to 1977. Therefore the TUE data were taken from the winter months December 1997 to February 1998 and December 1998 to February 1999. The data of [Buishand and Velds 1980] do not indicate zero daily amounts separately: so approximately 60% of the days had a daily amount of less than 1 mm. Our data show that approximately 40% of the days had no rain and approximately 20% had a rain amount between 0 and 1 mm. Apart from this possible difference, the figure shows quite a good agreement between the TUE rain data and the De Bilt rain data. We cannot state whether this agreement is fortuitous or not, because similar data for the weather station at Eindhoven Airport for a period of many years ($\geq$30 years) have not yet been published.

5.2.3 Horizontal rain measurements by two gauges and a disdrometer

Figure: Relative horizontal rain amounts measured at position P2 ( $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$) and P3 ( $\includegraphics[width=2em]{gen/m-streep.eps}$) corresponding to intervals of relative differences (formula 5.2) between 5-min rain intensities at these two positions. Period: 1 December 1997 to 30 November 1999.

On the roof of the Auditorium two tipping-bucket rain gauges were installed at positions P2 and P3, respectively (figure 3.4). The distance between these two positions is 33 m. The purpose of the two rain gauges is to investigate spatial differences in rain intensity on the roof. Figure 5.8 shows the horizontal rain amounts measured at P2 and P3 (normalised to the total rain amount) corresponding to relative differences of the rain intensity measured by the two gauges. These relative differences are defined as the difference in rain intensity divided by the mean rain intensity:

$$2 \frac{ R_{\text{h,c,\texttt{P2}}} - R_{\text{h,c,\texttt{P... ...{ R_{\text{h,c,\texttt{P2}}} + R_{\text{h,c,\texttt{P3}}} }.$$ (5.2)

From the figure one can deduce that the rain intensity difference is within 10% (30%) for approximately 52% (83%) of the total rain amount. These results are quite satisfactory, form which we conclude that the two positions P2 and P3 represent the same situation.

Figure 5.9: Cumulative horizontal rain amounts measured by a rain gauge at position P2 ( $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$), a rain gauge at position P3 ( $\includegraphics[width=2em]{gen/m-stippel.eps}$), and a distrometer (close to P3) ( $\includegraphics[width=2em]{gen/m-streep.eps}$). Based on 5-min data from 1-10-1999 to 7-1-2000.

Figure 5.10: Relative horizontal rain amounts measured by the rain gauge at P2 ( $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$) and by the disdrometer ( $\includegraphics[width=2em]{gen/m-streep.eps}$) corresponding to intervals of relative differences between 5-min rain intensities by these two devices. Period: 1-10-1999 to 7-1-2000.

At approximately 1.5 m from the rain gauge at position P3 a disdrometer was installed. The disdrometer was operational from 1-10-1999 to 7-1-2000. Figure 5.9 presents the cumulative horizontal rain amounts measured by the three devices during this period. Differences are within 30% on monthly basis. Remarkably, the amounts collected by the disdrometer seem larger than those collected by the two rain gauges.

A distribution of rain amounts over intervals of relative differences (cf. formula 5.2) between the gauge at P2 and the disdrometer for every 5-min clock period is plotted in figure 5.10. Almost 18% (46%) of the total horizontal rain amount is measured with less than 10% (30%) difference between the 5-min values of the rain gauge and the disdrometer. The figure also shows that the disdrometer measures quite a large rain amount during clock periods when the rain gauge measures no rain (i.e. when the relative difference equals $-2$). This explains figure 5.9, where we observed that the total amount of rain measured by the disdrometer is larger than the total amount of rain measured by the rain gauges. The implications of this observation are not clear, because the considered period comprises only almost three months (during which disdrometer data are missing from 12-20 December 1999) and because we do not have much experience with the disdrometer. It is possible that the disdrometer does not function totally well and its performance should be investigated in more detail.

Nevertheless, we conclude that the differences in reading between the rain gauge and the disdrometer are generally not so bad, because, as said before, the rain intensity difference is within 30% for approximately 46% of the total rain amount.

5.2.4 Rain spells

A rain spell is defined here as a period consisting of consecutive 5-min clock periods with $R_{\text{h,c}}>0.02$ mm h$^{-1}$. In figure 5.11, the cumulative relative distribution of rain spell durations measured at the Auditorium is plotted. Almost 50% of the rain spells take less than 25 min. In section 5.1, we noted that hourly rain intensity data should be applied with care, because they will give a poor indication of actual rain intensities, especially maxima. Figure 5.11 supports for this conclusion: rain spells are often shorter than an hour.

Figure 5.11: Cumulative relative distribution of rain spell durations measured at the Auditorium (position P2). Based on 5-min clock periods from 1-12-1997 to 30-11-1999.

From our measurements, we can also calculate the percentage of the time that rain occurs. This is approximately 8%. [Buishand and Velds 1980] mention a percentage of 7% for the Netherlands.

5.2.5 Driving rain amounts and intensities

Driving rain measurements were performed by two TUE-II type gauges. One of these gauges was placed at a central position on the west façade of the Main Building (positions P4 or P5; in short: P4/5), and the other TUE-II gauge was installed at the north edge of the façade (position P6). The reader is referred to figure 3.6 for a drawing of the exact positions.

Figure 5.12 shows the monthly driving rain amounts collected by the driving rain gauges at P4/5 and P6, respectively. The same information is listed in table 5.2. The driving rain gauge at the edge (P6) catches 1.1 to 4.3 times the driving rain amount of the central gauge (P4/5), and on average about 1.5 times as much.

Figure 5.12: Monthly driving rain amounts at position P4/5 ( $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$) and P6 ( $\includegraphics[width=2em]{gen/m-streep.eps}$) measured by TUE-II type driving rain gauges. Based on 5-min clock periods during 1-12-1997 to 30-11-1999. Note that the gauge at P6 was operational from 2 March 1998.

Figure 5.13: Driving rain amounts for various horizontal wind velocity intervals ($U_{\text {h}}$) and various wind direction ($\Phi$) intervals. Based on 5-min data measured from 1-12-1997 to 30-11-1999. Driving rain was measured by the TUE-II gauges at position P4/5 (fig. a) and position P6 (fig. b), respectively.

Figure 5.14: Driving rain intensities at P4/5 (fig. a&c) and P6 (fig. b&d) as a function of the wind velocity component perpendicular to the façade ($U_y$), for horizontal rain intensities $R_{\text {h,c,\texttt {P2}}}=$ 2.0-2.1 mm h$^{-1}$ ( $\includegraphics[width=0.5em]{gen/m-kruisje.eps}$) and 4.0-4.1 mm h$^{-1}$ ( $\includegraphics[width=0.5em]{gen/m-rondje.eps}$). Based on 5-min data from 1-12-1997 to 30-11-1999.

Figure 5.13a gives a distribution of driving rain measured by the TUE-II gauge at position P4/5 from December 1997 to November 1999, over intervals of reference wind speed and wind direction measured at the top of the mast on the Auditorium. Figure 5.13b shows the driving rain distribution for the north-edge west façade position P6. The edge catches especially more rain for wind speeds between 3 and 10 m s$^{-1}$ and for wind directions of NW and W.

Figure 5.14 shows 5-min driving rain intensities as a function of the wind velocity component perpendicular to the façade ($U_y$) for two narrow horizontal rain intensity intervals ( $R_{\text {h,c,\texttt {P2}}}$) and for the two positions P4/5 and P6. Note that the $x$ axis of the graphs represents $-U_y$ (with the minus) because only negative values of $U_y$ correspond to wind blowing towards the façade (see the axis definition in figures 2.4 and 3.4). As we expect, driving rain intensity increases with wind speed and horizontal rain intensity. However, one also concludes from these plots that driving rain intensities even show large variations for a particular wind speed and horizontal rain intensity. A factor which has not been measured and therefore is not taken into account here, is the raindrop spectrum. Variations of the raindrop spectrum might be the cause of a part of the variation in driving rain intensities. In section 5.3 the relation between wind speed, wind direction, horizontal rain intensity and driving rain intensity will be described in more detail.

Figure 5.15: Cumulative relative distribution of driving rain intensities, in terms of the number of 5-min clock periods with that intensity ( $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$) and the driving rain amount ( $\includegraphics[width=2em]{gen/m-streep.eps}$). Based on 5-min data measured by driving rain gauge TUE-II at positions P4/5 (fig. a) and P6 (fig. b) from 1-12-1997 to 30-11-1999. The median 5-min driving rain intensity (according to rain amounts) is also indicated.

Distributions of driving rain intensities are drawn in figures 5.15a for P4/5 and 5.15b for P6. Every figure has two lines and is similar to figure 5.6 (for horizontal rain). The solid line represents the cumulative relative distribution of 5-min clock periods with a particular driving rain intensity. The dashed line represents the cumulative relative distribution of the total driving rain amount contributed by all clock periods with a particular rain intensity. The medians at positions P4/5 and P6 are 0.67 and 1.0 mm h$^{-1}$, respectively. This suggests that the driving rain intensities at the façade edge (P6) are higher than at the central façade position (P4/5). The discussion on the differences between the two façade positions is continued in the following section.

5.2.6 Driving rain at two positions

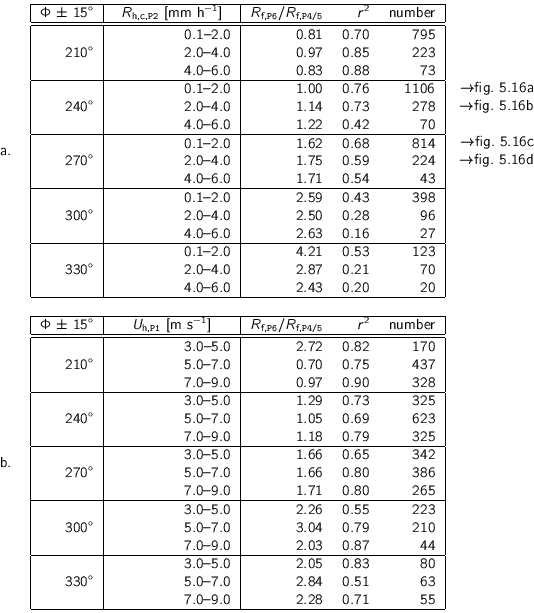
Table 5.4 lists the results of least-squares fits ($y=cx$) of correlations between the driving rain intensities measured at P4/5 and P6, respectively. The correlations are obtained from the data selected according to various wind direction intervals and horizontal rain intensity intervals (table 5.4a) and according to various wind direction intervals and wind speed intervals (table 5.4b). The intervals cannot be taken too small, because in that case the number of data points would be too low. For this reason, the data are not selected by the three parameters (wind direction, wind speed and rain intensity) together. Correlations with a selection based on the horizontal rain intensity and the wind speed component perpendicular to the façade ($U_y$) are not shown here, because these lead to very dispersed correlation plots.

Table: Correlations of $R_{\text {f,\texttt {P6}}}/R_{\text {f,\texttt {P4/5}}}$ for various wind direction intervals and horizontal rain intensity intervals (table a), and various wind direction intervals and horizontal wind speed intervals (table b). The last column lists the number of data points. Some of the correlations of table a are plotted in figure 5.16. Based on 5-min data from 1-12-1997 to 30-11-1999.

Figure 5.16: Correlations between 5-min driving rain intensities at position P4/5 and P6, for various wind direction intervals ($\Phi$, figures a&b versus c&d) and horizontal rain intensity intervals ( $R_{\text {h,c,\texttt {P2}}}$, figures a&c versus b&d). Period: 1-12-1997 to 30-11-1999.

Four correlations of table 5.4a are plotted in figure 5.16. From the figure and table 5.4a, one concludes that south-western wind (i.e. between 210$^\circ$ and 240$^\circ$) yields a ratio $R_{\text {f,\texttt {P6}}}/R_{\text {f,\texttt {P4/5}}}$ of approximately 1, and this ratio increases for western and north-western winds. The coefficient of determination ($r^2$) is worse for wind directions of 330$^\circ$ than for wind directions of 210$^\circ$ or 240$^\circ$. This is mainly due to a low number of data points, and perhaps also due to more variation caused by the turbulence at the façade edge near P6. Table 5.4a also shows that, generally, an increase of the horizontal rain intensity for a particular wind direction interval does not change the ratio $R_{\text {f,\texttt {P6}}}/R_{\text {f,\texttt {P4/5}}}$ much. At the wind direction interval of 330$^\circ$ the ratios are different for lower and higher rain intensities; this is due to the large scatter (and the small number of data) at the higher rain intensities. Table 5.4b lists the correlations of $R_{\text {f,\texttt {P6}}}/R_{\text {f,\texttt {P4/5}}}$ for various wind direction intervals and wind speed intervals. The ratios reveal no particular tendency for increasing wind speeds. Our data indicate that the wind direction has a much larger influence on the ratio, than wind speed and horizontal rain intensity.

5.2.7 Example of rainfall with high driving rain intensities

The year 1998 was an extremely wet year, so even the 1998 annual report of the KNMI was dedicated to rain [KNMI 1999]. The rain amounts of March, April, June, September, October and December 1998 were almost twice of the normal rain amounts. The yearly total was 1239.6 mm (normally 803 mm). At Eindhoven Airport the yearly total was 955.1 mm. At the Auditorium we measured 857.2 mm at P2 and 809.4 mm at P3. The Auditorium total is approximately 100 to 150 mm less than the Airport total, of which approximately 80 mm can be attributed to the malfunction of our devices during June 1998.

We measured a series of high driving rain intensities in September 1998 and October 1998. The driving rain gauge at P4/5 collected 6.1 mm of driving rain during 20 hours continuously on 14 and 15 September 1998 (the monthly driving rain amount was 8.5 mm). The reservoir of the driving rain gauge was emptied once during rain; this may have led to an error of 0.1 mm. Also much of the driving rain amount in October 1998 was collected in a short time. During 20 h on 27 and 28 October 1998 the gauge at P4/5 measured 6.0 mm. Unfortunately, the reservoir had to be emptied twice during rain, which may have led to an error of 0.4 mm. The total driving rain amount of October 1998 was 10.3 mm. Note that these mentioned errors relate to the exceptional cases in September and October 1998, when the reservoirs were (almost) overflowed. Of course, these errors are not typical for the normal functioning of the driving rain gauges.

Figure 5.17: Five-minute wind speeds and directions from 28-10-1998 (0h00) till 29-10-1998 (12h00).

Figure 5.18: Cumulative horizontal rain amounts (at P2) and driving rain amounts (at P4/5, $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$, and at P6, $\includegraphics[width=2em]{gen/m-streep.eps}$), from 28-10-1998 (0h00) till 29-10-1998 (12h00).

Figure 5.19: Five-minute horizontal rain intensities (at P2) and driving rain intensities (at P4/5 and P6), from 28-10-1998 (0h00) till 29-10-1998 (12h00).

For merely illustrative purposes, figures 5.17-5.19 show the wind speeds, wind directions, horizontal rain and driving rain (intensities as well as cumulative amounts) measured on 28-10-1998 and 29-10-1998. Remarkable for the presented rain events is that a sudden wind direction change towards 270$^\circ$ goes along with increasing horizontal rain and driving rain intensities, which reach very high peek values at 28-10-1998 on 10h25 and 29-10-1998 on 05h15. The dynamics of the horizontal rain and the driving rain were so high that the lower rain intensities in figure 5.19 are hardly visible.

5.2.8 Maximum horizontal rain and driving rain

Tables 5.5 and 5.6 list the ten 5-min clock periods with the highest driving rain intensities measured at position P4/5 and P6, respectively. The tables also list the horizontal rain intensities, wind speeds, wind directions and dates corresponding to the ten largest driving rain intensities. For every value of a quantity, except for the wind direction, its rank and its number of occurrence is indicated. A rank of 1 means that the value is the highest value. To avoid many ranking levels, the quantities were rounded to a tenth or to one. If the number of occurrence of a particular value is more than one, this means that the same value occurred several times. If the number of occurrence of a driving rain intensity value is more than one, the indicated date is the date of the first occurrence. The indicated dates (and times) give the start of the 5-min clock periods.

Table 5.5: The ten highest 5-min driving rain intensities at P4/5 from from 1-12-1997 to 30-11-1999, with the other parameters corresponding to the same 5-min clock period. The rank and the number of occurrence (#) of the actual values are also indicated. The indicated dates (and times) give the start of the 5-min clock periods. The units are mm h$^{-1}$ for rain intensities, m s$^{-1}$ for wind speeds and degrees from north for wind directions.

$R_{\text{f,\texttt{P4/5}}}$	29.3	17.8	15.7	13.0	10.5	9.6	7.2	6.7	6.4	6.0
rank	1	2	3	4	5	6	7	8	9	10
#	1	1	1	1	1	1	1	2	1	1
$R_{\text{f,\texttt{P6}}}$	-	-	24.9	17.5	9.9	16.5	8.6	-	10.3	4.9
rank	-	-	1	2	6	3	10	-	5	22
#	-	-	1	1	1	1	1	-	1	1
$R_{\text {h,c,\texttt {P2}}}$	46	31	31	41	45	28	50	33	22	34
rank	4	13	13	7	5	15	3	11	18	10
#	1	3	3	1	1	1	1	2	1	1
$R_{\text{h,c,\texttt{P3}}}$	53	29	30	40	48	27	50	30	20	25
rank	2	11	10	7	4	13	3	10	18	15
#	2	1	3	1	1	1	1	3	3	1
$U_{\text {h}}$	11.1	1.9	9.3	6.2	5.9	9.7	7.6	9.5	4.8	5.7
rank	47	139	65	96	99	61	82	63	110	101
#	43	2691	192	1600	1930	175	666	185	3184	2160
$\Phi$	269	245	278	260	253	263	221	208	256	223
$U_y$	11.1	1.7	9.3	6.1	5.7	9.7	4.9	4.5	4.7	3.9
rank	26	120	44	76	80	40	88	92	90	98
#	12	2778	61	498	684	52	1238	1458	1382	2084
year	1998	1998	1998	1998	1998	1998	1999	1998	1999	1999
month	10	1	10	9	8	6	6	1	2	8
day	28	7	29	9	26	2	3	3	21	18
hour	10	14	5	16	14	15	21	15	17	11
minute	30	0	15	55	35	55	55	25	40	20

Table 5.6: The ten highest 5-min driving rain intensities at P6 from from 1-12-1997 to 30-11-1999. See further the caption of table 5.5.

$R_{\text{f,\texttt{P4/5}}}$	15.7	13.0	9.6	3.8	6.4	10.5	3.8	4.2	3.7	7.2
rank	3	4	6	18	9	5	18	15	19	7
#	1	1	1	2	1	1	2	2	1	1
$R_{\text{f,\texttt{P6}}}$	24.9	17.5	16.5	12.6	10.3	9.9	9.6	9.4	9.3	8.6
rank	1	2	3	4	5	6	7	8	9	10
#	1	1	1	1	1	1	1	1	1	1
$R_{\text {h,c,\texttt {P2}}}$	31	41	28	19	22	45	17	59	20	50
rank	13	7	15	21	18	5	23	1	20	3
#	3	1	1	3	1	1	6	1	7	1
$R_{\text{h,c,\texttt{P3}}}$	30	40	27	18	20	48	17	58	18	50
rank	10	7	13	20	18	4	21	1	20	3
#	3	1	1	5	3	1	6	1	5	1
$U_{\text {h}}$	9.3	6.2	9.7	7.7	4.8	5.9	6.6	1.7	7.3	7.6
rank	65	96	61	81	110	99	92	141	85	82
#	192	1600	175	598	3184	1930	1291	2431	824	666
$\Phi$	278	260	263	283	256	253	292	262	294	221
$U_y$	9.3	6.1	9.7	7.5	4.7	5.7	6.2	1.7	6.7	4.9
rank	44	76	40	62	90	80	75	120	70	88
#	61	498	52	225	1382	684	489	2778	369	1238
year	1998	1998	1998	1998	1999	1998	1998	1999	1998	1999
month	10	9	6	10	2	8	8	7	8	6
day	29	9	2	28	21	26	22	4	24	3
hour	5	16	15	10	17	14	14	23	1	21
minute	15	55	55	25	40	35	50	30	40	55

The ten largest 5-min driving rain intensities at P4/5 are all unique occurrences (except for the 8th in rank, which occurred twice), and range from 6.0 to 29.3 mm h$^{-1}$. The corresponding horizontal rain intensities range from 22 to 53 mm h$^{-1}$, and are very high compared to the median of 2.2 mm h$^{-1}$ (see figure 5.6). The corresponding wind speeds range from 1.7 (!) to 11.1 m s$^{-1}$. One would expect that higher wind speeds and horizontal rain intensities would yield higher driving rain intensities, but this is not obvious for the events in table 5.5. Only the values of the wind speed components perpendicular to the façade ($U_y$) show a more distinct increasing tendency. Remarkable is that the second highest driving rain intensity occurred when the wind speed was only 1.9 m s$^{-1}$. A close inspection of the data of 7-1-1998 14h00 reveals that the previous clock period had a wind speed $U_y$ of 5.9 m s$^{-1}$ and a rain intensity of 1.2 mm h$^{-1}$. The next clock period had a wind speed $U_y$ of 8.5 m s$^{-1}$ and a rain intensity of 7.8 mm h$^{-1}$. It is therefore possible that the wind speed indicated in the table for 7-1-1998 14h00-14h05 is an error due to a time lag between the clocks in the two data acquisition systems (one for the rain measurements, the other for the wind measurements, see figure 3.19).

Table 5.5 also shows driving rain intensities at P6 corresponding to the ten highest driving rain intensities at P4/5. Note that the driving rain gauge at P6 was not operational at the time of the 5-min clock periods starting at 7-1-1998 14h00 and 3-1-1998 15h25. At 28-10-1998 10h30 the reservoir of the P6 driving rain gauge was emptied to prevent it from overflowing and thus the actual driving rain intensity at P6 could not be registered.

Table 5.6 shows the 10 highest driving rain intensities measured at position P6. The 10 highest driving rain intensities at P6 correspond to the 20 highest driving rain intensities at P4/5 (see the ranks in the second row in table 5.6). Similar to P4/5, one can conclude that the circumstances for very high driving rain intensities at P6 vary quite a lot and there is no evident correlation between the wind speed, the horizontal rain intensity and the driving rain intensity. Note that a two year measurement period is too short for decisive conclusions with respect to rain events with extreme driving rain, although the measurements were carried out during an extremely wet year. Nevertheless, the driving rain intensity values of tables 5.5 and 5.6 can be used as a guide for driving rain gauge design (cf. section 4.4).

5.2.9 Raindrop spectra

As was mentioned in section 5.2.3, the disdrometer was only operational from 1-10-1999 to 7-1-2000. Although this is a rather short period and only a small part coincides with the general 24-month measurement period, some (exemplary) results are presented here to demonstrate the temporal variability and the parameterisation of raindrop spectra. Table 5.7 lists the horizontal and driving rain amounts measured during the period when the disdrometer was operational. It shows that the driving rain amounts during this period were small.

Table 5.7: Horizontal rain amounts [mm] measured by the tipping-bucket rain gauges at P2 and P3 and by the disdrometer, and driving rain amounts [mm] at P4/5 and P6, per wind direction interval. The last column shows the number of 5-min periods with rain. Clock periods with $U_{\text {h}}<0.3$ m s$^{-1}$ are listed separately. Based on 5-min data from from 1-10-1999 to 7-1-2000. Cf. table 5.3.

	hor. rain			dr. rain
$\Phi$ $\pm$ 15$^\circ$	P2	P3	disdro	P4/5	P6	number
0$^\circ$	4.2	3.9	4.9	0.00	0.01	187
30$^\circ$	0.0	0.0	0.6	0.00	0.00	151
60$^\circ$	0.0	0.0	1.3	0.00	0.00	404
90$^\circ$	0.0	0.0	0.5	0.00	0.00	210
120$^\circ$	1.8	1.8	2.8	0.00	0.00	167
150$^\circ$	1.3	1.1	1.9	0.00	0.00	142
180$^\circ$	4.9	4.9	6.5	0.00	0.00	382
210$^\circ$	28.6	29.6	31.3	0.33	0.33	1488
240$^\circ$	20.0	20.5	24.8	1.25	1.60	1224
270$^\circ$	13.0	12.8	17.3	2.06	4.25	491
300$^\circ$	5.2	5.5	6.1	0.32	1.15	214
330$^\circ$	2.5	2.8	3.0	0.00	0.05	188
$U_{\text{h}}<$0.3 m s$^{-1}$	0.8	0.7	0.1	0.02	0.01	27
totals	82.2	83.5	101.0	3.97	7.38	5275

Figure 5.20 shows the measured horizontal raindrop mass flux spectra of an arbitrarily chosen period of rain. The plotted sequential 10-min spectra show the evolution of a rain period with its large changes of raindrop spectra and rain intensity.

Figure 5.20: Horizontal raindrop mass flux spectra $\varphi _{\text {h}}(D)$ as a function of time from 2-10-1999 13h00.

In chapter 6 we will use the raindrop spectrum parameterisation of [Wessels 1972]. He obtained a range of the parameter $A$ of the [Best 1950] spectrum formula (eq. 2.24). Ninety percent of his 533 observations at De Bilt (NL) had a value of $A$ ranging from 0.88 to 1.77. Here, we compare raindrop spectra measured with our disdrometer with raindrop spectra calculated with $A=0.88$ and $A=1.77$. The calculated raindrop spectra have the same horizontal rain intensity as the measured spectra. The purpose is to investigate how much the calculated spectra differ from actual spectra. Figure 5.21c shows a raindrop spectrum measured by the disdrometer during an arbitrary 5-min clock period. The asterisk indicates the median drop size. Figures 5.21a and 5.21b show the corresponding raindrop spectra calculated with $A=0.88$ and 1.77, respectively. They are obviously different from the measured spectrum.

Figure 5.21: Horizontal raindrop mass flux spectra $\varphi _{\text {h}}(D)$ with the same horizontal rain intensity (1.9 mm h$^{-1}$), (a) calculated from the parameterisation of [Wessels 1972] with $A=0.88$, (b) with $A=1.77$, and (c) measured by the disdrometer during an arbitrary 5-min clock period. The asterisk indicates the median drop size.

Figure 5.22: Correlation of median drop sizes measured by the disdrometer ( $D_{50,\text {disdro}}$) and calculated according to the parameterisations of [Wessels 1972], i.e. with $A=0.88$ ( $\includegraphics[height=0.5em]{gen/m-vierkant.eps}$) and $A=1.77$ ( $\includegraphics[angle=90,width=0.6em]{gen/m-ruit.eps}$). The measurements are based on 5-min data from 1-10-1999 to 7-1-2000 selected for $U_{\text {h}}=$ 3.5-11.2 m s$^{-1}$ and $\Phi =$ 270$^\circ$$\pm$15$^\circ$.

Figure 5.22 shows the correlation between the median drop size of the measured spectra ( $D_{50,\text {disdro}}$) and the median drop sizes of the two calculated raindrop spectra (with $A=0.88$, $\includegraphics[height=0.5em]{gen/m-vierkant.eps}$, and 1.77, $\includegraphics[angle=90,width=0.6em]{gen/m-ruit.eps}$). The median drop size was chosen to make differences in the spectra visible (yet to some extent). Figure 5.22 shows that generally the measured median drop size is between the two calculated median drop sizes (i.e. the straight line is between a $\includegraphics[height=0.5em]{gen/m-vierkant.eps}$ and a $\includegraphics[angle=90,width=0.6em]{gen/m-ruit.eps}$ at the same $D_{50,\text {disdro}}$). However, for larger median drop sizes the measured median drop size becomes larger than the calculated median drop sizes. This indicates that the measured drop spectra contain more larger drops than the spectra calculated with the given parameters (cf. figure 5.21). From the figure we conclude that the measured raindrop spectra come close to the two parameterisations of [Wessels 1972], but that the parameterisations have a tendency to underestimate the number of large drops. [Schönhuber et al. 2000] measured raindrop spectra of a few storm events in a moderate climate with a two-dimensional video-disdrometer. These few measurements revealed a considerable number of large drops up to 8 mm (more than one expects from the [Marshall and Palmer 1948] spectra) and seem to support our suggestion that the number of large drops is underestimated by relations like those of [Marshall and Palmer 1948] and [Best 1950].