6.4 Results of driving rain calculations

Results of rain simulations are presented and discussed in the same order as the calculations, i.e. firstly catch ratios $\eta (D)$ on the west façade of the Main Building and, secondly, driving rain amounts on the façade. Finally, the driving rain simulations are compared with driving rain measurements.

Catch ratios $\eta (D)$ Figure 6.10 shows simulated catch ratios $\eta (D)$ on the west façade of the Main Building for $U_{\text {h}} = 3.5$ m s$^{-1}$ and wind from the west. The calculations included turbulent dispersion of drops. From the figure one can observe that, for a given drop diameter, the upper part of the façade has higher catch ratios than the lower part. This applies also for the sides of the west façade in comparison to the middle part. Besides, the catch ratio on a façade section increases with drop diameter (figure 6.10) and with wind speed (cf. figures 6.10 and 6.12).

When the turbulent drop dispersion is not included in the calculations, the results are as shown in figure 6.11. Compared to the calculations with dispersion, these results show lower values of $\eta (D)$. The relative differences are larger for smaller $D$. It seems that drops more easily hit the façade when turbulent dispersion is included in the calculations. Turbulence can be seen as an extra mechanism which drives drops out of their `mean paths' which are determined by the mean wind velocity and the drop's inertia. However, the calculation of the turbulent drop dispersion in the $K$-$\epsilon$ model assumes isotropic turbulence, which is not realistic near surfaces. This means that the simulated turbulent velocity component perpendicular to the façade might be too large and the lateral turbulent component too small. Because of their smaller inertia, larger drops are less sensitive to turbulence than smaller drops, and therefore the difference in $\eta$ of larger drops with and without turbulent dispersion is smaller.

Exemplary drop trajectories in figure 6.3 also illustrate the differences between smaller and larger drops, and between calculations with and without turbulent drop dispersion.

Figure 6.10: Simulated catch ratios $\eta (D)$ on the west façade of the Main Building, for $U_{\text {h}} = 3.5$ m s$^{-1}$ and $\Phi = 270$$^\circ$. Calculations with turbulent dispersion of drops.

Figure 6.11: As figure 6.10, but without turbulent dispersion of drops.

Figure 6.12: As figure 6.10, but with $U_{\text {h}} = 5.7$ m s$^{-1}$.

Figure 6.13: Simulated catch ratios $\eta (D)$ at façade sections A1-E1 (solid lines in figure a), A18-E18 (dashed lines in a), A7-E7 (solid lines in b) and A12-E12 (dashed lines in b). Cf. figure 6.10. Configuration: $U_{\text {h}} = 3.5$ m s$^{-1}$ and $\Phi = 270$$^\circ$, with turbulent drop dispersion. See figure 6.2 for the positions of the façade sections.

Figure 6.14: As figure 6.13, but without turbulent drop dispersion. Cf. figure 6.11.

The simulated catch ratios $\eta (D)$ at several façade sections as a function of drop diameter are depicted in figures 6.13 (with drop dispersion) and 6.14 (without drop dispersion). In figures 6.13a and 6.14a, solid lines refer to façade sections A1, B1, etc. to E1, whereas the dashed lines refer to façade sections A18, B18, etc. to E18, which are their symmetric counterparts. Figures 6.13b and 6.14b present the results of façade sections A7 to E7 and A12 to E12, respectively. By showing the symmetrical counterparts of the façade sections in one figure, we can see the variations in $\eta (D)$ at symmetrical façade sections. These variations are larger when a façade section is located more to the edges, and can be explained by the higher degree of turbulence at the edges of the building, and by computational errors in the wind and drop trajectory simulations.

Comparing the results of the calculations with and without turbulent drop dispersion, one can see that especially drops of smaller sizes do not hit the façade on the lower façade sections at all when drop dispersion is not included. Moreover, $\eta (D)$ is generally lower without drop dispersion than with drop dispersion.

Figure 6.15: Raindrop mass flux spectra with rain intensities of 0.1, 1.0 and 3.0 mm h$^{-1}$ respectively, according to the parameterisation of [Wessels 1972]: $A$ = 0.88 ( $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$) and 1.77 ( $\includegraphics[width=2em]{gen/m-stippel.eps}$), $a=0.21$, $b=2.25$, $C=67$, and $q=0.846$ (eq. 2.24). $\Delta D$ = 0.1 mm.

Figure 6.16: Simulated driving rain ratio $k$ on the west façade of the Main Building, for $U_{\text {h}} = 3.5$ m s$^{-1}$, $\Phi = 270$$^\circ$, trajectory calculations with turbulent drop dispersion, and the raindrop spectrum of [Wessels 1972] with $A=0.88$ (see $\includegraphics[width=2em]{gen/m-ononderbroken.eps}$ in figure 6.15).

Figure 6.17: As figure 6.16, but without turbulent drop dispersion.

Figure 6.18: As figure 6.16 but based on raindrop spectra with $A=1.77$ (see $\includegraphics[width=2em]{gen/m-stippel.eps}$ in figure 6.15).

Figure 6.19: As figure 6.17 but based on raindrop spectra with $A=1.77$.

Driving rain ratio $k$ The chosen raindrop spectra for the calculation of driving rain ratios ( $k = R_{\text{f}}/R_{\text{h}}$) are depicted in figure 6.15. As mentioned in section 6.2, the parameterisation of [Wessels 1972] is used. Figures 6.16 to 6.19 show the driving rain ratios $k$ for the various façade sections and the two values of $A$. As one can expect from the above observations on $\eta (D)$, the driving rain ratio is higher at the upper and side edges of the building, and for rain spectra with relatively more larger drops. Moreover, the differences in $\eta$ resulting from the inclusion of turbulent dispersion are also apparent in $k$.

Figure: Simulation of driving rain intensities based on CFD calculations of drop trajectories and based on data of full-scale measurements. The resulting driving rain intensity is compared with the corresponding measured values in figures 6.21-6.23.

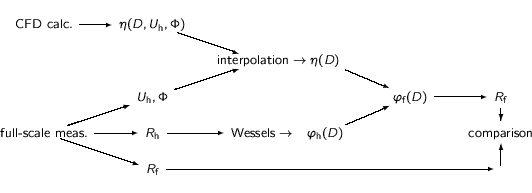Comparison with measured driving rain intensities A scheme of the driving rain intensity calculations is presented in figure 6.20. Using the [Wessels 1972] parameterisations, the raindrop mass flux spectra ( $\varphi _{\text {h}}(D)$) are calculated from the horizontal rain intensity obtained from the full-scale measurements. Catch ratios ($\eta (D)$) for a particular façade section, reference wind speed and direction are obtained by interpolation of the catch ratios obtained by the raindrop trajectory (CFD) calculations. As these calculations were not performed for every possible reference wind speed and direction, we can only calculate $\eta (D)$ and, subsequently, $\varphi_{\text{f}}(D)$ for limited ranges of wind speeds and directions. (The actually performed CFD calculations are listed in table 6.2.) The results presented below are obtained by the method described in this paragraph and depicted in figure 6.20.

The plots in figure 6.21 show measured and simulated driving rain intensities at position P4/5 as a function of horizontal rain intensity. The full-scale measurement data in figure 6.21a result from selection for $\Phi =$ 270$^\circ$$\pm$15$^\circ$ and $U_{\text {h}}=$ 4-5 m s$^{-1}$, while the simulated data were obtained from calculations with turbulent drop dispersion. The simulated data show that different raindrop spectrum parameters result in different driving rain intensities for a given horizontal rain intensity, wind speed, wind direction and façade position. Moreover, a given spectrum parameterisation yields an almost linear relation between horizontal and driving rain intensities. This relation can be expressed by the following formula:

$$R_{\text{f}} \; = \; \int \eta(D) \varphi_{\text{h}}(D,A,R_{\text{h}}) dD \; \approx \; k(A) R_{\text{h}},$$ (6.10)

where $\varphi_{\text{h}}(D,A,R_{\text{h}})$ is the raindrop mass flux spectrum as a function of the [Best 1950] raindrop spectrum parameters $A$ and $R_{\text {h}}$ (eq. 2.24).

Figure 6.21: Driving rain intensities as a function of horizontal rain intensities, at position P4/5; for $\Phi =$ 270$^\circ$$\pm$15$^\circ$, and for $U_{\text {h}}=$ 4-5 m s$^{-1}$ (figures a&b) or 7-8 m s$^{-1}$ (figure c). The measurements are indicated by $\includegraphics[width=0.5em]{gen/m-iksje.eps}$ and based on 5-min values from 1-12-1997 to 30-11-1999. The simulations are indicated by $\includegraphics[height=0.5em]{gen/m-vierkant.eps}$ and $\includegraphics[angle=90,width=0.6em]{gen/m-ruit.eps}$ and based on measured $R_{\text {h}}$ and Wessels' spectra with $A=0.88$ and $A=1.77$, respectively. In figures b&c, the simulations do not include turbulent drop dispersion (n.t.d.), whereas in figure a it is included (w.t.d.). Note the different scale of the $y$ coordinate in figure c.

Figure 6.22: As figure 6.21, but for position P6.

Figure 6.21a and equation 6.10 show that the driving rain ratio ($k$) for given façade position, wind speed and wind direction is a function of parameter $A$, which determines the shape of the raindrop spectrum. In other words, raindrop spectra with the same horizontal rain intensity but with different shapes yield different driving rain intensities. The measured data are very scattered and differ often much from the simulated data. Of course, the real raindrop spectra are unknown, and hence could not be used in the calculations. We know that it is very likely that measured raindrop spectra differ much from relations like those given by [Best 1950] (see section 5.2.9). Hence, we cannot yet conclude whether the relation of equation 6.10 corresponds to reality. Moreover, it is possible that the simulated catch ratio $\eta (D)$ do not correspond to the actual situation because of errors in the simulation of wind speeds and raindrop trajectories. Other causes for the scatter may be, for instance, the applied clock period, the temporal evolution of rain events, and the neglect of raindrop coagulation in the model. At the end of this section we will show results of driving rain intensities calculated directly from measured raindrop spectra.

The simulation shown in figure 6.21b differs only from the one in figure 6.21a by the fact that no turbulent drop dispersion is used. The difference between the two simulation results in figure 6.21b, i.e. corresponding to the two parameterisations of the raindrop spectra, is now much larger. Thus, without turbulent drop dispersion, the influence of differences in drop spectra (i.e. in $A$) has a larger effect than with turbulent drop dispersion. This is explained by differences in the catch ratios $\eta (D)$ (e.g. figure 6.13 and 6.14 respectively). Small drops have a smaller tendency to fall onto the façade in calculations without turbulent drop dispersion, and therefore the ratio between the number of smaller and bigger drops, which is quite large in the chosen raindrop spectrum parameterisations (see figure 6.15), results in larger differences in the simulated driving rain intensities.

The simulation shown in figure 6.21c differs only from the one in figure 6.21b by the reference wind speed, namely 7-8 m s$^{-1}$. As expected, higher wind speeds result in higher driving rain intensities. Comparing the results of the measurements with the results of the simulations presented in figures 6.21a-c, we see that many measurements fall outside the region enclosed by the simulated data which represent 90% of all drop spectra in the Netherlands according to [Wessels 1972]. The simulation may even systematically overestimate (figure 6.21a) or underestimate (figure 6.21c) the measurements by a factor of 2.

Figure 6.22 shows the results for position P6 in the same way as figure 6.21 for position P4/5. More or less the same conclusions as given above hold position P6.

Figure 6.23: Correlation of driving rain intensities at positions P4/5 and P6; for $\Phi =$ 270$^\circ$$\pm$15$^\circ$, and for $U_{\text {h}}=$ 4-5 m s$^{-1}$ (figures a&b) and 7-8 m s$^{-1}$ (figure c). The measurements are indicated by $\includegraphics[width=0.5em]{gen/m-iksje.eps}$ and based on 5-min values from 1-12-1997 to 30-11-1999. The simulations are indicated by $\includegraphics[height=0.5em]{gen/m-vierkant.eps}$ and $\includegraphics[angle=90,width=0.6em]{gen/m-ruit.eps}$ and based on measured $R_{\text {h}}$ and Wessels' spectra with $A=0.88$ and $A=1.77$, respectively. In figures b&c, the simulations do not include turbulent drop dispersion (n.t.d.), whereas in figure a it is included (w.t.d.).

The results of simulations without and with turbulent drop dispersion for a given position, wind speed and wind direction can be compared by comparing figure 6.21a with figure 6.21b, and figure 6.22a with figure 6.22b. The figures show that the simulations with turbulent drop dispersion result in higher driving rain intensities than those without turbulent drop dispersion. If one projects all results presented in the figures 6.21a and b (and in the figures 6.22a and b respectively) into one figure, many measured data fall within the region comprised by the simulated data. As we also have seen before, a simulation with turbulent drop dispersion yields larger driving rain intensities than without turbulent drop dispersion. Due to the fluctuating velocity components, more drops impinge on the façade than in simulations without turbulent drop dispersion, and hence the driving rain intensity is higher. Moreover, the trajectory model with the turbulent drop dispersion may likely overestimate the number of drops on the façade because it is based on isotropic turbulence, and therefore on too high estimates of fluctuating velocity components perpendicular to the façade. Comparing the simulations with the measurements, it seems indeed that the two raindrop trajectory models yield an upper and lower limit.

Comparison between P4/5 and P6 A correlation of the measured and simulated driving rain intensities at positions P4/5 and with those at P6 is plotted in figure 6.23. Figure 6.23a corresponds to figures 6.21a & 6.22a and, likewise, figure 6.23b with 6.21b & 6.22b and figure 6.23c with 6.21c & 6.22c. As we have observed that the relation between horizontal rain intensity and simulated driving rain intensity is almost linear (eq. 6.10 and figs. 6.21 and 6.22), it is obvious that the simulated data in figure 6.23 form a straight line too. The ratio between the simulated driving rain intensities at P4/5 and P6 is therefore almost independent of raindrop spectrum parameterisation. The measured data are, however, very much scattered. The measured ratios $R_{\text {f,\texttt {P6}}}/R_{\text {f,\texttt {P4/5}}}$ (compare also with table 5.4b) are generally larger than the simulated ratios. Here again, it is difficult to trace back where inaccuracies were introduced in the simulations.

Figure 6.24: Driving rain intensities at positions P4/5 and P6: $\includegraphics[height=0.5em]{gen/m-vierkant.eps}$ & $\includegraphics[angle=90,width=0.6em]{gen/m-ruit.eps}$, simulated with $R_{\text {h,disdro}}$ and Wessels' parameterisations with $A=0.88$ and $A=1.77$ respectively; $\includegraphics[width=0.6em]{gen/m-sterretje.eps}$, simulated with measured raindrop spectra ( $\varphi _{\text {h, disdro}}(D)$); and $\includegraphics[width=0.5em]{gen/m-iksje.eps}$, measured. The horizontal rain intensity $R_{\text {h,disdro}}$ is based on 5-min measurements by the disdrometer from 1-10-1999 to 7-1-2000, selected for $\Phi =$ 270$^\circ$$\pm$15$^\circ$ and for $U_{\text {h}}=$ 3.5-11.2 m s$^{-1}$. The simulations do not include turbulent drop dispersion (n.t.d.).

Measured raindrop spectra Figure 6.24 shows the results of driving rain intensities calculated from our measured raindrop spectra. The disdrometer was only operational during a short period (1-10-1999 to 7-1-2000). Therefore the range of the selected wind speeds was extended to 3.5-11.2 m s$^{-1}$ to obtain enough data. The data indicated by $\includegraphics[height=0.5em]{gen/m-vierkant.eps}$ and $\includegraphics[angle=90,width=0.6em]{gen/m-ruit.eps}$ represent the calculations based on Wessels' spectra with $A=0.88$ and $A=1.77$, respectively, and with horizontal rain intensities measured by the disdrometer ( $R_{\text {h,disdro}}$). The calculations indicated by $\includegraphics[width=0.6em]{gen/m-sterretje.eps}$ are based directly on the measured raindrop spectra ( $\varphi _{\text {h, disdro}}(D)$), so not totally similar to figure 6.20. Important to note is that the simulation results based on the measured raindrop spectra ( $\includegraphics[width=0.6em]{gen/m-sterretje.eps}$) show much more scatter than the other simulation results ( $\includegraphics[height=0.5em]{gen/m-vierkant.eps}$ and $\includegraphics[angle=90,width=0.6em]{gen/m-ruit.eps}$). The measured driving rain intensities are indicated by $\includegraphics[width=0.5em]{gen/m-iksje.eps}$. The figure shows that the simulated driving rain intensities differ from the measured driving rain intensities. However, in the case of position P4/5 the simulations based on the measured raindrop spectra and those based on the Wessels' parameterisation with $A=1.77$ are quite close to the measurements. In the case of position P6 almost all simulated data are lower than the measured driving rain data. Although the number of measurements with the disdrometer is small, we intend to conclude that the best parameterisation of the raindrop spectrum by Wessels is the one with $A=1.77$.