Next: 2.3 Driving rain Up: 2. Theory Previous: 2.1 Wind Contents
Precipitation occurs when cloud particles, which grow in complex processes like condensation and aggregation, reach such a size that their falling velocity is larger than the upward wind speed in the air. Precipitation is called rain when its particles are liquid water at ground level. Apart from its complex formation in clouds, rain is basically a population of falling drops interacting with each other (collision, breakup) and with their environment (wind, evaporation).
General literature on rain can be found in for example [Pruppacher and Klett 1978]. For climatological information on rain one can refer to [Buishand and Velds 1980] for the Netherlands.
In a first approximation, the minimum size of raindrops falling on the ground
depends on vertical wind speeds in clouds.
In clouds with updraughts of less than 50
cm s![]() , drops of 0.2 mm (terminal velocity of 70 cm s
, drops of 0.2 mm (terminal velocity of 70 cm s![]() )
and more will fall out. In air of 90% humidity such a drop can
fall 150 m before total evaporation and thus reach the ground.
A drop of 1 mm can fall 40 km.
Rain which mainly consists of drops of 0.1 mm diameter, is called drizzle,
and is produced by low layer clouds.
)
and more will fall out. In air of 90% humidity such a drop can
fall 150 m before total evaporation and thus reach the ground.
A drop of 1 mm can fall 40 km.
Rain which mainly consists of drops of 0.1 mm diameter, is called drizzle,
and is produced by low layer clouds.
The maximum diameter of raindrops is about 7 mm, because larger drops will break apart during the fall.
Only drops of diameters of less than 0.3 mm are nearly perfect spheres at terminal (falling) velocity. Therefore for larger drops one can not unambiguously describe the shape by one length. This problem is solved by the definition of a equivalent diameter: the diameter of a sphere with the same volume as the deformed drop.
Falling drops of (equivalent) diameters of 0.3 to 1 mm resemble oblate spheroids. Drops larger than 1 mm resemble oblate spheroids with flat bases (figure 2.5).
![\begin{center}%
\psfrag{0.8} [Bc]{0.8}
\psfrag{2.7} [Bc]{2.7}
\psfrag{5.8}...
...hics[width=0.3\linewidth]{h-theory/eps/shape-of-raindrops.eps}%
\end{center}](img197.gif) |
In the following sections and chapters, the term ``diameter'' should be understood as the ``equivalent diameter''. Moreover, one should keep in mind that raindrop diameters range from 0.1 mm to 7 mm. The number of raindrops per drop size in rainfall (``raindrop spectrum'') is discussed in section 2.2.4.
The velocity of a drop depends on gravitation and drag due to wind speed.
The motion of a drop can be described by:
Figure 2.6 shows the drag coefficient ![]() as function of the
Reynolds number. The function of [Morsi and
Alexander 1972] was obtained from fitting
a large amount of laboratory data for different kinds of particles, from
different references. Data on falling water drops in still air obtained by
[Gunn and
Kinzer 1949] have been included in the graph. For falling drops
as function of the
Reynolds number. The function of [Morsi and
Alexander 1972] was obtained from fitting
a large amount of laboratory data for different kinds of particles, from
different references. Data on falling water drops in still air obtained by
[Gunn and
Kinzer 1949] have been included in the graph. For falling drops ![]() mm
(
mm
(![]()
![]() 10
10![]() ), the drag coefficient is underestimated by [Morsi and
Alexander 1972].
), the drag coefficient is underestimated by [Morsi and
Alexander 1972].
![\begin{center}%
%%% x-axis [cc][b]
%%% y-axis [Bc][t]
\psfrag{reynoldsnumber...
...cludegraphics[height=\matlabhoogte]{h-theory/cd/dragcoeff.eps}%
\end{center}](img211.gif) |
The terminal velocity is the maximum vertical velocity which a drop reaches. It is, in other words, the velocity when the gravitational force equals the drag force. The usual assumption that the vertical velocity approximately equals the terminal velocity, is thus only valid in wind flow with zero vertical wind velocity. Generally this is a good approximation for the undisturbed wind flow far from obstacles; near buildings vertical wind velocity influences the drop velocity. Strictly speaking, the horizontal wind component could also influence the falling velocity because it can deform the shape of a raindrop and thus the drag.
[Gunn and
Kinzer 1949] presented a table with terminal velocity data as
a function of drop diameter, measured in laboratory. We fitted these data with
the following function:
Often one applies such a relation obtained from
laboratory experiments in still air at an air pressure of 760 mm Hg, a temperature
of 20![]() C and a relative humidity of 50%.
In figure 2.7 the relation given by eq. 2.11 is
plotted, with terminal velocities calculated directly from the equation of motion
(eq. 2.10) and drag coefficients of [Morsi and
Alexander 1972].
The latter method overestimates the terminal velocity of
bigger drops (
C and a relative humidity of 50%.
In figure 2.7 the relation given by eq. 2.11 is
plotted, with terminal velocities calculated directly from the equation of motion
(eq. 2.10) and drag coefficients of [Morsi and
Alexander 1972].
The latter method overestimates the terminal velocity of
bigger drops (![]() mm), because the used drag coefficient function does
not take drop deformation into account.
mm), because the used drag coefficient function does
not take drop deformation into account.
![\begin{center}%
%%% x-axis [cc][b]
%%% y-axis [Bc][t]
\psfrag{D [mm]} [cc][b...
...s[height=\matlabhoogte]{h-theory/fitgunn/terminalvelocity.eps}%
\end{center}](img215.gif) |
The stopping distance
![]() is the distance travelled by
a drop as a result of its inertia, after the driving force is suddenly
taken away [Fuchs 1964]. In our case, the driving force is the wind
speed. The stopping distance is a function of the drop diameter
is the distance travelled by
a drop as a result of its inertia, after the driving force is suddenly
taken away [Fuchs 1964]. In our case, the driving force is the wind
speed. The stopping distance is a function of the drop diameter ![]() and
the initial speed
and
the initial speed ![]() of the drop and can be calculated by use of
equation 2.10 with the conditions
of the drop and can be calculated by use of
equation 2.10 with the conditions ![]() ,
, ![]() and
and
![]() . The solution is:
. The solution is:
Figure 2.8a shows the stopping distance for various initial
speeds (cf. wind speeds) and various drop diameters, calculated with
values of ![]() given by [Morsi and
Alexander 1972]. The same figure gives
results calculated with
given by [Morsi and
Alexander 1972]. The same figure gives
results calculated with ![]() values of [Gunn and
Kinzer 1949], as far as the
limited range of Reynolds numbers allowed for (cf. figure 2.6).
Figure 2.8b shows the same information as figure
2.8a, but now condensed into two lines, as is obvious from eq.
2.12.
values of [Gunn and
Kinzer 1949], as far as the
limited range of Reynolds numbers allowed for (cf. figure 2.6).
Figure 2.8b shows the same information as figure
2.8a, but now condensed into two lines, as is obvious from eq.
2.12.
![% midden\{%
\small
% begin\{tabbing\}
a.
%%% x-axis [cc][b]
\psfrag{Uwind...
...]{h-theory/stopweg-martin/stopdistance-dim3.eps}}
%
% end\{tabbing\}
% \}
\par](img223.gif) |
The stopping distance is a measure for the ability of raindrops to
follow changes in wind speed and direction. In general, in eddies where
wind flow is curved and accelerated, the stopping distance can
characterise the dispersion of raindrops, i.e. the raindrop trajectory
deviations from the wind pattern. Raindrops with a certain
![]() will follow eddies with a certain minimum
dimension, say
will follow eddies with a certain minimum
dimension, say
![]() , but eddies with a dimension
smaller than
, but eddies with a dimension
smaller than
![]() will hardly or not effect the
raindrop trajectory. We will assume here that
will hardly or not effect the
raindrop trajectory. We will assume here that
![]() approximately equals
approximately equals
![]() .
.
The integral length scale, ![]() , is an estimate of the dimensions of
the largest eddies in a neutral homogeneous boundary layer. Estimates
range from 50 to 200 m [Geurts 1997].
Figure 2.8 shows that for wind speeds up to 10 m s
, is an estimate of the dimensions of
the largest eddies in a neutral homogeneous boundary layer. Estimates
range from 50 to 200 m [Geurts 1997].
Figure 2.8 shows that for wind speeds up to 10 m s![]() the
stopping distance is less than
the
stopping distance is less than ![]() , and that the drops will follow
such eddies. Close to buildings we will find smaller eddies, for
example a frontal vortex with the dimension of the building height (see
section 2.1.4 for other typical
values).
, and that the drops will follow
such eddies. Close to buildings we will find smaller eddies, for
example a frontal vortex with the dimension of the building height (see
section 2.1.4 for other typical
values).
Without a numerical model it is not easy to estimate how the raindrops
will be dispersed by eddies other than ![]() or a frontal vortex.
[]p. 201]crowe:1998 cite an estimation for the length
scale of a turbulent eddy within the framework of the
or a frontal vortex.
[]p. 201]crowe:1998 cite an estimation for the length
scale of a turbulent eddy within the framework of the ![]() -
-![]() turbulence model for the fluid:
turbulence model for the fluid:
| (2.14) |
Although the relation
![]() is
only a crude approximation, we conclude that dispersion of raindrops due to the
turbulence of the wind is very likely an important factor.
is
only a crude approximation, we conclude that dispersion of raindrops due to the
turbulence of the wind is very likely an important factor.
Rain is characterised by raindrop spectra. In meteorology raindrop spectra
(also called ``raindrop distributions'') are often expressed in a number of
drops per (volume) unit of air per (equivalent) drop diameter. It is here
called ``raindrop number concentration spectrum'', denoted by ![]() and
its unit is m
and
its unit is m![]() m
m![]() .
.
For our purposes, it is more practical to express
raindrop spectra in terms of mass fluxes on or through a certain area. First
we define a raindrop mass concentration spectrum ![]() [kg m
[kg m![]() m
m![]() ]:
]:
Subsequently, a raindrop mass flux spectrum
![]() [kg m
[kg m![]() s
s![]() m
m![]() ] through the horizontal is defined by:
] through the horizontal is defined by:
Relation 2.16 is only valid (1) if the vertical velocity of every drop equals the terminal velocity (and is not affected by vertical wind, turbulence and raindrop interaction), and (2) if the raindrop spectrum does not depend on time and location (i.e. in stationary rainfall). [Uijlenhoet and Stricker 1999] gave an extensive overview of different definitions of raindrop spectra and their integral quantities.
Raindrop mass flux spectra give a better impression of
the contribution of every drop size to the total rain amount. This amount
is expressed by the horizontal rain intensity ![]() [mm h
[mm h![]() ]
and is defined by the amount of rain water falling through a horizontal
plane per hour in the undisturbed wind flow, and equals
the summation of the mass fluxes of all drops falling through the plane:
]
and is defined by the amount of rain water falling through a horizontal
plane per hour in the undisturbed wind flow, and equals
the summation of the mass fluxes of all drops falling through the plane:
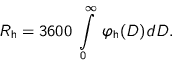 |
(2.17) |
Three other quantities are sometimes used, namely (1) the liquid water
content ![]() [kg m
[kg m![]() ], i.e. the amount of liquid water per unit of air:
], i.e. the amount of liquid water per unit of air:
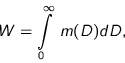 |
(2.18) |
Three frequently used empirical formulae for raindrop spectra are presented in the following.
[Marshall and
Palmer 1948] spectra
Probably the most widely used empirical description of raindrop spectra
is that of [Marshall and
Palmer 1948]:
[Marshall and
Palmer 1948] obtained ![]() and
and ![]() from measurements amongst
others by
[Laws and
Parsons 1943], who describe in detail the measurement and
averaging methods used at that time:
from measurements amongst
others by
[Laws and
Parsons 1943], who describe in detail the measurement and
averaging methods used at that time:
Examples of [Marshall and Palmer 1948] spectra are plotted in figure 2.9a. We converted these raindrop size spectra into raindrop mass flux spectra and the result is plotted in figure 2.9b. Comparison of figures a and b shows that a mass flux spectrum gives a better impression of the contribution of every drop size to the total rain amount on the horizontal.
Subsequent studies pointed out that the parameters ![]() and
and ![]() vary widely (and even during rainfall). One has tried to classify these
parameters by the type of rain, as e.g. in [Joss and
Waldvogel 1969] (table
2.2).
vary widely (and even during rainfall). One has tried to classify these
parameters by the type of rain, as e.g. in [Joss and
Waldvogel 1969] (table
2.2).
| type of rainfall | ||
| [m |
[ |
|
| drizzle | 30 000 |
|
| widespread | 7 000 |
|
| thunderstorm | 1 400 |
|
![\begin{center}%
\psfrag{diameter[mm]} [cc][b]{\small$D$ [mm]}
\psfrag{numbe...
....44\linewidth]{h-theory/best/mp_massflux.eps} \\
\end{tabular} \end{center}](img249.gif) |
[Marshall and
Palmer 1948] obtained the parameterisation
2.22 by analysing rainfall with drops of 1 to 3.5 mm diameter
and with rain intensities of 1 to 23 mm h![]() . It is therefore often
assumed that this parameterisation overestimates of
the number of drops below 1 mm diameter. Therefore, other spectra (e.g. gamma
distributions) were proposed. An overview is given in
[Sempere
Torres and Porrà 1994].
. It is therefore often
assumed that this parameterisation overestimates of
the number of drops below 1 mm diameter. Therefore, other spectra (e.g. gamma
distributions) were proposed. An overview is given in
[Sempere
Torres and Porrà 1994].
[Ulbrich 1983] spectra
The raindrop spectrum of [Ulbrich 1983] is defined as:
![\begin{center}%
%%% x-axis [cc][b]
\psfrag{diameter[mm]} [cc][b]{$D$ [mm]}
...
...degraphics[height=\matlabhoogte]{h-theory/best/comp_mp_ul.eps}%
\end{center}](img251.gif) |
The Ulbrich spectrum includes an extra parameter (![]() ), which should
take variations in
), which should
take variations in ![]() (of eq. 2.21) into account. E.g.
[Waldvogel 1974] showed that large and sudden changes in
(of eq. 2.21) into account. E.g.
[Waldvogel 1974] showed that large and sudden changes in ![]() can
occur from moment to moment within a given rainfall type.
Figure 2.10 shows examples of Ulbrich spectra. Note that for
can
occur from moment to moment within a given rainfall type.
Figure 2.10 shows examples of Ulbrich spectra. Note that for
![]() the Ulbrich spectrum equals the Marshall-Palmer spectrum.
the Ulbrich spectrum equals the Marshall-Palmer spectrum.
![\begin{center}%
%%% x-axis [cc][b]
\psfrag{diameter[mm]} [cc][b]{$D$ [mm]}
...
...aphics[height=\matlabhoogte]{h-theory/best/best-wessels-3.eps}%
\end{center}](img253.gif) |
[Best 1950] spectra
The third type of raindrop spectrum presented here, was proposed by
[Best 1950]. The spectrum is expressed by:
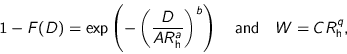
The values of the constants ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() were obtained from
results of measurements in Great-Britain and eight papers (e.g.
[Laws and
Parsons 1943] and [Marshall and
Palmer 1948]), and amount to 1.30, 0.232, 2.25,
67 and 0.846, respectively. The [Best 1950] spectrum is used in
[Wessels 1972] to analyse raindrop spectra measured at De Bilt (NL) during
1968 and 1969. The best regression of the 533 observations was found with
were obtained from
results of measurements in Great-Britain and eight papers (e.g.
[Laws and
Parsons 1943] and [Marshall and
Palmer 1948]), and amount to 1.30, 0.232, 2.25,
67 and 0.846, respectively. The [Best 1950] spectrum is used in
[Wessels 1972] to analyse raindrop spectra measured at De Bilt (NL) during
1968 and 1969. The best regression of the 533 observations was found with
![]() and
and ![]() . 90% of the observations had a constant
. 90% of the observations had a constant ![]() ranging
from 0.88 to 1.77 (with
ranging
from 0.88 to 1.77 (with ![]() ). Individual raindrop spectra can thus vary
widely in shape, as is illustrated in figure 2.11.
). Individual raindrop spectra can thus vary
widely in shape, as is illustrated in figure 2.11.
Summary
The three presented raindrop spectra can be summarised by the following
formula for the raindrop mass concentration spectrum:
| Marshall and Palmer: |
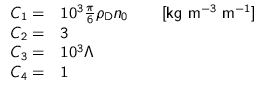 |
| Ulbrich: |
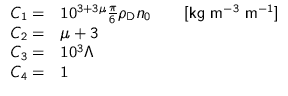 |
| Best: |
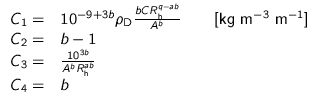 |
| Note that in eq. 2.24:
|
© 2002 Fabien J.R. van Mook