2.1 Wind

Wind around a building causes driving rain on the envelope of the building. Without wind there is no driving rain. The atmospheric boundary layer (a.b.l.) is the layer close to the Earth's surface, in which wind is directly influenced by friction with the Earth's surface. Its height ranges from hundreds of metres to a few kilometres and depends on the intensity of thermal mixing (convection), terrain roughness and latitude. The atmospheric surface layer (a.s.l.) is the lowest 10-20% of the a.b.l., where shear is approximately constant with height and production of turbulence is high. The a.s.l. over a uniform flat terrain in a neutral boundary layer is characterised by a wind velocity increasing with height and a wind direction being nearly constant with height.

Due to spatial changes in surface roughness, internal boundary layers (i.b.l.) develop, in which wind speed and direction are modified by the properties of the surface (obstacles), while the top of the i.b.l. flow is the wind velocity adjusted to the terrain conditions before the roughness change. The thickness of the i.b.l. increases downstream of the roughness change.

In the following we will only pay attention to a neutral boundary layer, i.e. an atmospheric situation in which vertical heat transfer is negligible.

2.1.1 Mean wind speed in the a.s.l.

The mean wind speed in the a.s.l. as a function of height is expressed by the so-called ``logarithmic law'':

$$\bar{u}(z) = \frac{u_{\ast}}{\text{\fontfamily{computermode... ...tfont\itshape k}} \ln \left( \frac{z - d}{z_{0}} \right),$$ (2.1)

where $\bar{u}(z)$ is the mean horizontal wind speed [m s$^{-1}$] at $z$ [m] height from ground level, $u_{\ast}$ the friction velocity [m s$^{-1}$], $\text{\fontfamily{computermodern}\selectfont\itshape k}$ the von Kármán constant (0.4), $d$ the displacement height [m], and $z_0$ the aerodynamic roughness length [m].

The friction velocity $u_{\ast}$ is defined by:

$$\tau_0 = \rho u_{\ast}^2,$$ (2.2)

and can be measured in the a.s.l. from:

$$u_{\ast} = - \sqrt{\overline{u' w'}},$$ (2.3)

where $\tau_0$ is the surface shear stress [N m$^{-2}$] (i.e. drag force per unit of area), $\rho$ the air density [kg m$^{-3}$], and $u'$ and $w'$ are the fluctuating components of the longitudinal and vertical wind velocities, respectively.

Displacement height and roughness length are measures for the roughness of a terrain. A classification of typical $z_0$ values is presented in Wieringa ([Wieringa 1992], [Wieringa 1996]). Some typical values are listed here:

$z_0$ [m]	landscape
0.0002	open sea or lake
0.03	flat terrain with grass, airport runways
0.10	moderately open country with low vegetation and occasional obstacles separated by more than 20 obstacle heights $\mathcal{H}$ (e.g. low hedges, single rows of trees)
1.0	closed and regularly covered terrain; open spaces up to $\mathcal{H}$ (e.g. city, mature forests)

The logarithmic law (eq. 2.1) applies only for:

• homogeneous and stationary flow. The fetch with a homogeneous surface roughness should be at least 10 to 20 km,

• neutrally stable atmospheric conditions,

• heights $z$ in the ranges

  $\bullet$

  $z > 20 z_0 + d$,

  $\bullet$

  $z<z_{\text{a.s.l.}}$, where $z_{\text{a.s.l.}}$ is the height of the a.s.l., and

• positions far from buildings, i.e. at distances $> 2.5\mathcal{H}$ above the building, $> 12\mathcal{H}$ in the wake of the building, and $> 3\mathcal{H}$ upstream (with $\mathcal{H}$ denoting building height).

2.1.2 Change of terrain roughness

In the literature one finds several approaches for a relation between wind above two adjacent terrains with different roughness properties. Here, we investigate an abrupt roughness change according to two models. Figure 2.1 sketches the situation. The quantities on the terrain upwind from the change will be denoted by index 1, downwind by index 2.

Figure 2.1: Development of a internal boundary layer (i.b.l.) and change of mean wind profiles due to a roughness change. Wind is coming from the left.

Internal boundary layer model According to the internal boundary layer model described in [Simiu and Scanlan 1996], it is suggested that the wind velocity at the top of the i.b.l. ( $h_{\text{i.b.l.}}$) on the second terrain equals the velocity at the same height on the first terrain.

The height of the i.b.l. at a distance $x$ [m] from the roughness change is [Simiu and Scanlan 1996, p. 73]:

$$h_{\text{i.b.l.}}(x) = 0.28 {z_0}_{\text{max}} \left( \frac{x}{{z_0}_{\text{max}}} \right)^{0.8},$$ (2.4)

with ${z_0}_{\text{max}}$ = the largest value of ${z_0}_1$ and ${z_0}_2$.

An example is given to calculate the wind speed at a position A at 45 m above ground level in a town (denoted by $u_{2}(45)$) with a known wind speed at 10 m height at a weather station outside the town ($u_{1}(10)$). The distance from A to the town border is $x=5$ km. The weather station is on grass covered terrain, so ${z_0}_{1}=0.03$ m. The roughness of the town is ${z_0}_{2}=1$ m and the displacement height is $d_{2}=10$ m. So, position A at 45 m height is above $20 {z_0}_{2} + d_{2}$. According to equation 2.4, $h_{\text{i.b.l.}}$ equals 250 m. The relationship between the mean wind speeds at 10 m and 250 m height at the weather station is calculated from the logarithmic law:

$$u_{1}(250) = \frac{{u_{\ast}}_{1}}{\text{\fontfamily{comput... ...font\itshape k}} \ln \left( \frac{10}{{z_{0}}_{1}} \right).$$

This yields $u_{1}(250) = 1.6 u_{1}(10)$.

According to the i.b.l. model the wind velocity at A at i.b.l. height $h_{\text{i.b.l.}}(250)$ approximates the wind velocity at the weather station at the same height, so:

$$u_{2}(250) = u_{1}(250), \quad \text{and} \quad u_{2}(250)... ...ont\itshape k}} \ln \left( \frac{250}{{z_{0}}_{2}} \right).$$

The wind speed at 45 m height at A is:

$$u_{2}(45) = \frac{{u_{\ast}}_{2}}{\text{\fontfamily{compute... ...font\itshape k}} \ln \left( \frac{45}{{z_{0}}_{2}} \right),$$

which yields in this example: $u_{2}(45) = 1.08 u_{1}(10)$.

Similarity model The second approach is referred to as the similarity model [Simiu and Scanlan 1996, p. 48]; the ratio of friction velocities is empirically estimated from the ratio of roughness lengths:

$$\frac{{u_{\ast}}_{2}}{{u_{\ast}}_{1}} = \left( \frac{{z_0}_{2}}{{z_0}_{1}} \right)^{0.0706}.$$ (2.5)

For the above example, this approach yields $u_{2}(45) = 0.78 u_{1}(10)$.

The present example shows that the two methods yield different results. The example reflects the site used in the study reported in this thesis. Measurements at this site yield $u_{2}(45) = 1.13 u_{1}(10)$ according to [Geurts 1997] and $u_{2}(45) = 0.90 u_{1}(10)$ according to our own measurements (see section 5.2.1). These values differ $\sim$20% from each other and the estimations differ to a similar extent. This is an indication of the error that has to be taken into account when estimating weather station vs. local wind speed ratios. (Note that for this example changing ${z_0}_{2}$ into 1.5 m and/or ${z_0}_{2}$ into 0.1 m will yield a difference of 3-10% in the estimated ratios.) The ratio $u_{2}(45)/u_{1}(10)$ at our site is discussed in [de Wit et al. 2002] too.

2.1.3 Turbulence in the a.s.l.

Turbulence in wind causes variation of wind velocity in time and space. Turbulence is often considered as a superposition of eddies with different sizes transported by the mean flow. The simplest characterisation of turbulence is by turbulence intensity, defined as the ratio of the root-mean-square of the fluctuating component of the longitudinal wind velocity and its time-averaged value:

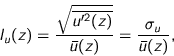$$I_u(z) = \frac{ \sqrt{\overline{u'^2(z)}} }{ \bar{u}(z) } = \frac{ \sigma_{u} }{ \bar{u}(z) },$$ (2.6)

where $I_u(z)$ is the longitudinal turbulence intensity [-] at elevation $z$ m, $u'(z)$ the fluctuating component of the longitudinal wind velocity [m s$^{-1}$], i.e. $u(z) = \bar{u}(z) + u'(z)$.

Similarly one defines lateral and vertical turbulent intensities $I_v(z)$ and $I_w(z)$, respectively.

The total mean turbulent kinetic energy $K$ (per unit of mass) is defined as:

$$K = 0.5 \left( \sigma_{u}^2 + \sigma_{v}^2 + \sigma_{w}^2 \right).$$ (2.7)

As shear is approximately constant with height in the a.s.l., the friction velocity $u_{\ast}$ is also approximately constant. The standard deviation of wind speed normalised by $u_{\ast}$ is therefore also a measure of turbulence in the a.s.l. Typical values, obtained by measurements, are presented in table 2.1.

Table 2.1: Typical values of standard deviations of wind velocity and mean turbulent kinetic energy in the a.s.l., obtained by measurements.

	[Panofsky and Dutton 1984]	[Geurts 1997]
${ \sigma_{u} }/{ u_{\ast} }$	2.4	2.41
${ \sigma_{v} }/{ u_{\ast} }$	1.9	1.91
${ \sigma_{w} }/{ u_{\ast} }$	1.25	1.37
${ K }/{ u_{\ast}^2 }$	5.5

2.1.4 Flow near buildings and urban canopy

Figure 2.2: Wind near a wide building [Beranek 1994b].

In the previous subsections we focussed on undisturbed wind. Describing wind patterns nearby buildings and in urban canopies (i.e. beneath the average roof height in towns) is quite difficult because many parameters and especially topography and building geometry are involved. Beranek ([Beranek 1994b], [Beranek 1994a]) and [Bottema 1993b] discuss this topic. We will first discuss the most important characteristics of the flow nearby a free standing building, bearing in mind that these characteristics should be useful for the evaluation of CFD simulations and that for a study on driving rain the lee side of a building is less interesting. Figure 2.2 shows a sketch of the time averaged wind pattern nearby a wide building in the atmospheric boundary layer. Its characteristics are (for more details, see e.g. []p. 80 and further]bottema:1993):

• a frontal vortex, i.e. recirculating flow at the windward side of a building. Its size depends mainly on the building height ($\mathcal{H}$), building width ($\mathcal{W}$) and the approach flow angle, and is of the order of $\mathcal{L}_g$, i.e. the smaller of $2\mathcal{H}$ and $\mathcal{W}$, for wind approaching perpendicularly to the façade. For buildings with $\mathcal{W}/\mathcal{H}\gg 3$, however, its size is about $\mathcal{H}$.
• corner streams are the zones near corners with higher wind speeds (higher than the approach wind speed at building height) and lower turbulence intensities.
• separation at corners occurs at the lateral faces of a building. The separation starts on the edge itself, if the corner is sharp. Downstream of the separation the flow can reattach to the lateral face.
• recirculation zones at the lee side are characterised by turbulent and very unsteady flow. They extend to approximately $4\mathcal{L}_g$ behind the building.

Figure 2.3: Computed 2-dimensional flow patterns which are typical flow regimes in building groups [Bottema 1993b]: a. $S_x/h = 1$ skimming flow, b. $S_x/h = 4$ wake interference flow, c. $S_x/h = 8$ isolated roughness flow.

The complexity of flows in building groups is of course larger than near a single building on an unbuilt plane. Yet three typical flow regimes are distinguished, depending on the ratio of building height and distance between the buildings. Figure 2.3 shows these for a two dimensional configuration.

2.1.5 Axis system definitions

We use two definitions for the wind velocity vector. The first one, which we will use most frequently, is a globally defined axis system, i.e. relative to north (see figure 2.4):

• the positive velocity components $U_x$ and $U_y$ are due north and due west, respectively. The positive component $U_z$ is directed upwards;
• the wind direction $\Phi$ is the angle in a horizontal plane from which the wind comes, expressed in degrees clockwise from north.

Figure 2.4: Global wind axis system: the definition of wind velocity components $U_x, U_y, U_z$, horizontal wind speed $U_{\text {h}}$ and horizontal wind direction $\Phi$.

The following quantities are derived from the wind velocity components:

• the horizontal wind speed:
  

  $$U_{\text{h}} = \sqrt{U_x^2 + U_y^2};$$ (2.8)

  
  

• the (absolute) wind speed:
  

  $$U = \sqrt{U_x^2 + U_y^2 + U_z^2}.$$ (2.9)

  
  

The second definition is related to the mean wind direction:

• the longitudinal wind velocity $u$ is parallel to the mean horizontal wind direction (thus: $u = U_{\text{h}}$);
• the lateral wind velocity $v$ is perpendicular to the mean horizontal wind direction (thus: $\bar{v} = 0$);
• the vertical wind velocity $w$ is directed upwards (thus: $w$ = $U_z$).